Linearly Independent(선형 독립)
* 만약 $R^n$ 차원의 벡터 {v1, v2, ... , vp} 들이 $x_1v_1, + x_2v_2 + ... + x_pv_p = 0$일 때(1.5에서 살펴본 Ax=0 형태의 homogeneous system이다), 1개의 trivial solution 즉, x=0의 해를 가질 때 linearly independent라고 한다.
Linearly Dependent(선형 의존)
* 만약 $R^n$ 차원의 벡터 {v1, v2, ... , vp} 들이 $x_1v_1, + x_2v_2 + ... + x_pv_p = 0$일 때, linearly independent와 달리 해 x가 not all zero, 즉 한 개라도 zero가 아닐 경우엔 linearly dependent라고 한다.
* 이 경우 해가 무수히 많은 nontrivial solution이 존재하게 된다.
* 만약 주어진 vector들로 augmented matrix를 구성하여 row reduction을 시행했을 때 free variable이 존재하면 nontrivial solution을 가지게 되므로 linearly dependent하다고 바로 알 수 있다.
Example 1)

* 위 vector들이 linearly independent한지 여부를 살펴보겠다. linearly independency를 살펴보기 위하여 vector v1,v2,v3를 사용하여 Ax=0 형태의 homogeneous system을 구성한 다음 augmented matrix형태로 변환하겠다.


* row reduction을 통해 reduced echelon form을 생성했다.
* basic variable은 x1, x2이고, free variable은 x3이다. $x_1=2x_3, x_2=-x_3$이기 때문에 solution x는 $x_3\begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix}$가 된다.
* 이미 free variable이 존재하기 때문에 linearly independent하다는 것을 알 수 있지만, 실제로 살펴보면 free variable $x_3$에 1이 온다면 $2v_1 - v_2 + v_3 = 0$이 되기 때문에 linearly independent하지 않다.
Linear Independence of matrix columns
* 만약 R^n space에 있는 vector $a_1, a_2, ... , a_n$로 구성된 $matrix A=[a_1 a_2 ... a_n]$ 가 존재할 때, Ax=0이 trivial solution을 가지고 있으면 linearly independent하다(그 역도 성립한다).
Sets of One Vector
$x_1 v = 0$
* vector v 1개로 구성된 homogeneous set은 v가 0이 아닐 경우 linearly independent하다.
* vector v가 0이라면 nontrivial solution이 존재하기 때문에 무수히 많은 해가 존재하게 될 것이다. 이는 free variable이 존재하고 linearly dependent하다는 것을 뜻한다.
* 하지만, vector v가 0이 아니라면 trivial solution만 존재하기 때문에 linearly independent하다.
Sets of Two Vectors
$v_1=cv_2$
$v_1 - cv_2 = 0$
* 두 개의 vector v1, v2 가 존재할 때 한 vector가 다른 vector의 곱으로 표현 가능하다면, 두 vector는 linearly dependent하다.
* 한 vector를 이항했을 때 coefficient들이 all zero가 아니기 때문이다. 만약 곱으로 표현되는 관계가 아니라면 trivial solution만 존재하기 때문에 linearly independent하다.
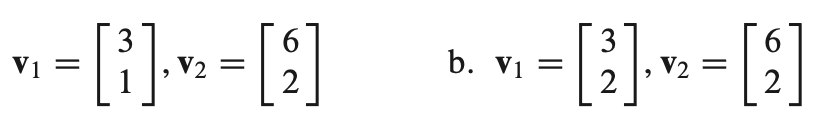
* 왼쪽의 경우 $2v_1 - v_2 = 0$
* 오른쪽의 경우 $x_1v_1 + x_2v_2 = 0$, x= (0,0)
Theorem 7. Characterization of linearly dependent sets
vector set S에 p개의 vector들이 존재할 때($S={v_1 ... v_p}$) 만약 특정 vector가 다른 vector들의 linear combination으로 표현될 수 있다면 해당 vector set S는 linearly dependent하다.
$c_1v_1 + c_2v_2 + ... + c_p v_p = 0$
* 위와 같은 linear system이 있다고 해보자. 만약 특정 vector가 $v_1$이라고 할 때 $v_1$이 다른 vector들의 linear combination으로 표현되기 위해서는 $c_1v_1$항을 이항하고 나머지 vector들이 속해있는 변을 $c_1$으로 나눠야한다. $c_1$으로 나누기 위해서는 $c_1$이 0이 아니어야 한다. 이 때문에 이 linear system은 nontrivial solution을 가지게 되고, 이에 따라 자동적으로 linearly dependent하다고 할 수 있지만, 수식으로 증명해보자.
$v_1 = (-c_2/c_1)v_2 + ... + (-c_p/c_1)v_p$
$-v_1-(c_2/c_1)v_2 - ... -(c_p/c_1)v_p = 0$
* 결국 $v_1$의 계수가 -1이 되어서 linearly dependent하다는 것을 알 수 있게 되었다.
$c_1v_1 + ... + c_pv_p = 0$
j: the largest subscription for which $c_j \neq 0$
$c_1v_1 + ... + c_jv_j + 0v_{j+1} + ... + 0v_p = 0$
* 그리고 만약 vector set S가 linearly dependent하고, v1의 coefficient $c_1$이 0이 아니라면, 어떤 $v_j(단, j>1)$는 $v_1, ... , v_{j-1}$의 linear combination으로 표현 가능하다.
$v_j = (-\frac{c_1}{c_j})v_1 + ... + (-\frac{c_{j-1}}{c_j})v_j-1$
* 위에서 $c_1$이 0이 아니라면 이라는 조건이 붙은 이유는 적어도 $c_1$이 0이 아니면 나머지가 다 0이라도 $v_1$이 남아 linear combination을 충족시킬 수 있기 때문이다.
* 이러한 성질은 아래 성질에 적용될 수 있다.
w가 Span{u,v}에 있으면, {u,v,w}는 linearly dependent하다. 역도 성립한다.
* 만약 w가 Span{u,v}에 있으면 $w = cu + dv$, $-w + cu + dv = 0$이 되기 때문에 not all zero 조건에 의해 linearly dependent하다고 볼 수 있다.
* 역으로 {u,v,w}가 linearly dependent하다면, $u \neq 0, v \neq 0$이고, u,v벡터는 한 벡터가 다른 벡터의 scalar multiplication으로 표현될 수 없기 때문에 w는 u,v혹은 u,u의 linear combination으로 표현된다. 즉, w는 Span{u,v}에 존재하게 된다.
Theorem 8
* 만약 vector set이 entry들보다 많은 vector를 포함하고 있으면, 다시말해 row의 개수가 column 개수보다 적다면 linearly dependent하다. pivot position이 부족해 free variable이 무조건 존자하게 되고, 그에 따라 nontrivial solution을 가지게 되기 때문이다.
Theorem 9.
* 만약 vector set이 zero vector를 포함하고 있다면, zero vector앞에 어떤 coefficient라도 올 수 있기 때문에 해당 vecrtor set은 linearly dependent하다.
정리
Linearly Dependent
* vector set이 존재할 때
* Homogeneous system의 solution이 nontrivial solution = Linearly Dependent
Linearly Independent
* vector set이 존재할 때
* Homogeneous system의 solution이 trivial solution = Lineary Independent
'수학 > Linear Algebra and its application' 카테고리의 다른 글
| 1.9 The Matrix of a Linear Transformation (0) | 2021.12.20 |
|---|---|
| 1.8 Introduction To Linear Transformations (0) | 2021.12.20 |
| 1.5 Solution Sets of Linear Systems (0) | 2021.12.15 |
| 1.4 The Matrix Equation (0) | 2021.12.13 |
| 1.3 Vector Equations (0) | 2021.12.13 |



