The matrix equation Ax=b

* A가 $R^{m \times n}$ space에 있는 matrix이고(n개의 vector로 구성된), x가 $R^n$ space에 있는 vector라고 했을 때 곱셈은 위와 같이 이뤄진다.
* 그리고 그 결과 값은 $R^m$ space의 vector가 된다.
* 실제 matrix와 vector로 예를 들면 아래와 같이 계산된다.
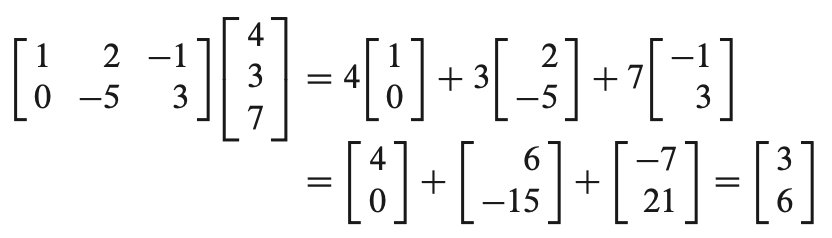
Theorem 3
- if A is an m x n matrix, with columns $a_1, ..., a_n$, and if b is in $R^m$
matrix equation Ax = b
vector equation $x_1a_1 + x_2a_2 + ... + x_na_n = b$
augmented matrix $[a_1 a_2 ... a_n b]$
- has same solution set.
Therom 4
- Let A be an m x n matrix,
1) For each b in $R^m$, the equation Ax=b has a solution.
2) Each b in $R^m$ is a linear combination of the columns of A.
3) The columns of A span R^m.
4) A has a pivot position in every row.
- 위 명제들은 모두 logically equivalent하며 하나의 명제가 틀릴 경우 모든 명제가 성립하지 않는다.
- 더 자세히 살펴보면 이러하다.
- 1,2 명제는 $R^m$ space의 모든 Ax=b에 대해 해가 있다는 것을 뜻한다.
- 이에 따라 3 명제가 성립하여 A는 $R^m$ space를 span한다고 할 수 있다.
- 4 명제는 1 명제에서 도출된 것이다. 1 명제가 참이라면(Ax=b has a solution) matrix A에는 [0, ..., 0 b]에 해당하는 row가 없기 때문이다. 때문에 모든 row에는 pivot position이 존재한다.
Therom 5
If A is an m x n matrix. u and v are vectors in $R^n$ and c is a scalar. then :
A(u+v)=Au+Av
A(cu)=c()
'수학 > Linear Algebra and its application' 카테고리의 다른 글
| 1.7 Linear Independence (0) | 2021.12.20 |
|---|---|
| 1.5 Solution Sets of Linear Systems (0) | 2021.12.15 |
| 1.3 Vector Equations (0) | 2021.12.13 |
| 1.2 Row Reduction and Echelon form (0) | 2021.12.12 |
| 1.1 Systems of Linear Equation (0) | 2021.12.12 |



