Homogeneous Linear System(동차선형계)
* A가 m x n matrix이고, 0은 Rn 차원의 vector라고 했을 때, Ax=0 형태로 나타내어지는 linear system을 Homogeneous Linear system이라고 한다.
* 이 경우 해는 2가지 경우가 존재한다. 첫 번째는 x=0이다. 이 solution은 너무도 당연한 solution이라는 뜻에서 trivial solution이라는 이름으로 불린다.
* 두 번째 경우는 무수히 많은 해가 존재할 경우이다. free variable이 하나라도 있다면, nontrivial solution 즉, 무수히 많은 해가 존재하게 된다.
Exercise 1) Determine whether there is a nontrivial solution

* 위와 같은 homogeneous system이 존재할 때 nontrivial solution이 있는지 확인해보자.


* row reduction을 통해 reduced echelon form을 생성하였다.
* 이에 따라 pivot position에 있는 x1, x2는 basic variable이고 x3는 free variable이다. x1=34x3 이고, x2=0 이다. 즉, 이 homogeneous system은 nontrivial solution을 가지고 있다.

* 조금 더 살펴보자면 이 system의 general solution은 위와 같이 x3과 vector의 곱으로서 표현할 수 있다.
* x3은 free variable이기 때문에 어떤 수도 올 수 있다. 처음에 주어진 homogeneous system의 general solution은 vector v가 나타낼 수 있는 공간인 span {v}의 어떤 값이라도 가질 수 있는 것이다. 즉, 주어진 system의 solution은 span{v}라고 간략하게 표현하는 것도 가능해진다.

* 즉 위 그림과 같이 3차원 공간에서의 직선으로 solution이 표시될 수 있는 것이다.
Exercise 2) Given Linear equation, describe all solutions.

* 위 equation의 x1은 basic variable이고, x2, x3는 free variable이다.

* 때문에 general solution을 위와 같이 나타낼 수 있다. exercise 1)에서 보았듯이 위와 같은 경우 general solution은 span {u, v}라고 할 수 있다.
Exercise Conclusion)
* homogeneous system의 solution은 항상 spanv1,v2,...,vp 로 나타낼 수 있다.
* 만약 trivial solution만 존재한다고 해도 span{0}이기 때문에 위 결론을 적용할 수 있다.
Solutions of Nonhomogeneous System(비동차선형계)
Nonhomogeneous linear system
* nonhomogeneous linear system은 Ax=b의 형태로 표현된다.
Exercise 1) Describe all solutions

* Ax=b가 위 예시를 따를 때 가능한 solution은 아래와 같다.


* nonhomogeneous system의 solution은 x=p+x3v, 일반화 하면 x=p+tv이다.
* 위 예제의 matrix A는 homogeneous system의 예제에서 봤던 matrix A이다. homogeneous system의 general solution은 우리가 방금 도출해 낸 nonhomogeneous system의 general solution인 x3v와 같았다. 즉, nonhomogeneous system의 general solution은 homogeneous system의 general solution에 vector p를 더한 것과 같다는 사실을 알 수 있다.

* 이를 기하학적으로 살펴보자면 위와 같다. homogeneous system의 solution인 span{v}를 뜻하는 직선을 vector p만큼 이동시킨 것이 nonhomogeneous system의 solution인 것이다.
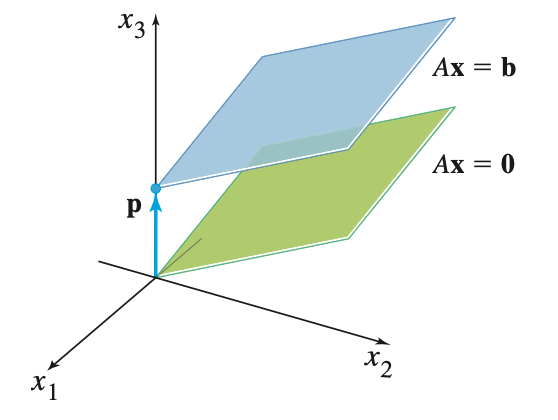
* 3차원 공간에서 살펴보자면 위와 같다.
Theorem 6.
Ax=b is consistent
and let p be a solution,
Then the solution set of Ax=b is the set of all vectors of the form
w=p+vh
where vh is any solution of the homogeneous equation Ax=0
정리
Homogeneous System
solution 경우의 수
1) nontrivial solution
* free variable이 존재(모든 column에 pivot 존재)
* infinitely many solutions
2) trivial solution
* free variable이 존재하지 않음(모든 column에 pivot 존재하지 않음)
* solution vector의 모든 entry가 0
'수학 > Linear Algebra and its application' 카테고리의 다른 글
| 1.8 Introduction To Linear Transformations (0) | 2021.12.20 |
|---|---|
| 1.7 Linear Independence (0) | 2021.12.20 |
| 1.4 The Matrix Equation (0) | 2021.12.13 |
| 1.3 Vector Equations (0) | 2021.12.13 |
| 1.2 Row Reduction and Echelon form (0) | 2021.12.12 |



