Matrix Multiplication

* vector에 matrix를 곱하는 것은 vector를 다른 차원의 space로 이동시키는 것과 같다.
Transformation

* 어떤 vector의 space를 이동시키는 transformation(function, mapping으로 부를 수도 있음)은 vector x를 $R^n$ space에서 $R^m$ space의 T(x)에 할당하는 것과 같다.
* T(x)를 x의 image라고 하고, image의 모든 셋을 뜻하는 T를 range라고 한다.
* Transformation의 표기는 아래와 같이 3가지로 표현 가능하다.
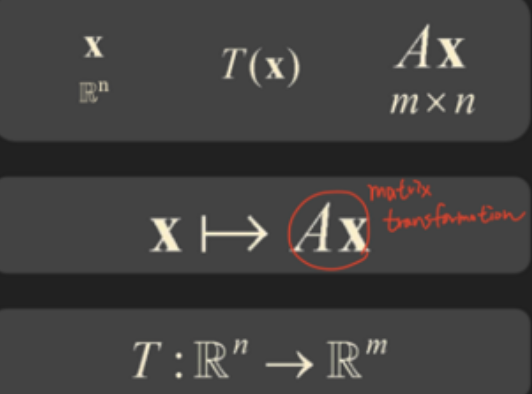
Example1) 동일한 차원에서의 transformation


* 3차원 vector를 3차원 space에 transformation했다. 결과적으로 $x_3$값이 0인 평면으로 transformation했다.



* 두 번째 transformation은 2차원 vector를 2차원 공간으로 transformation하는 경우다. 이러한 transformation을 shear transformation이라고 부른다. shear transformation은 물리학, 지질학, 결정학 등에서 사용되는 개념이다.
Example 2)



* T(u) + T(v) = T(u+v)라는 것을 알 수 있다.
Conclusion
* 모든 matrix transformation은 linear transformation이다.
'수학 > Linear Algebra and its application' 카테고리의 다른 글
| 2.1 Matrix Operations (0) | 2021.12.22 |
|---|---|
| 1.9 The Matrix of a Linear Transformation (0) | 2021.12.20 |
| 1.7 Linear Independence (0) | 2021.12.20 |
| 1.5 Solution Sets of Linear Systems (0) | 2021.12.15 |
| 1.4 The Matrix Equation (0) | 2021.12.13 |



