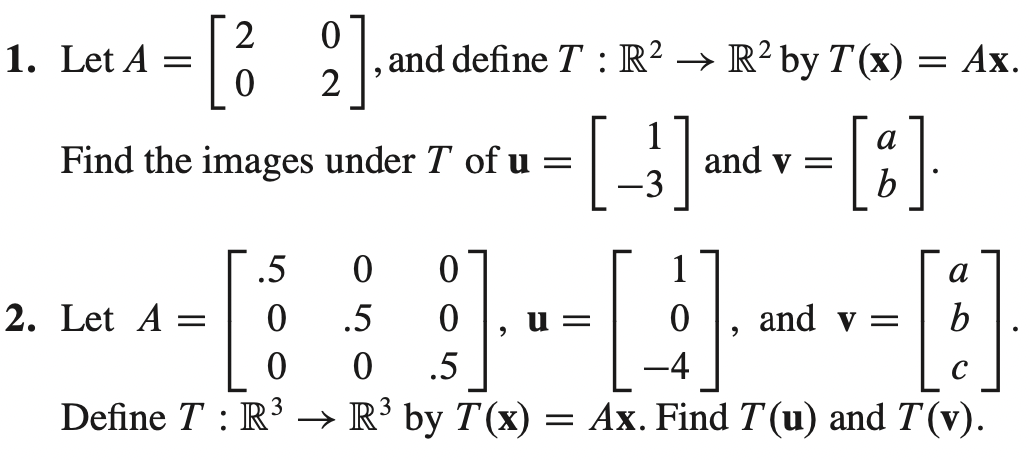
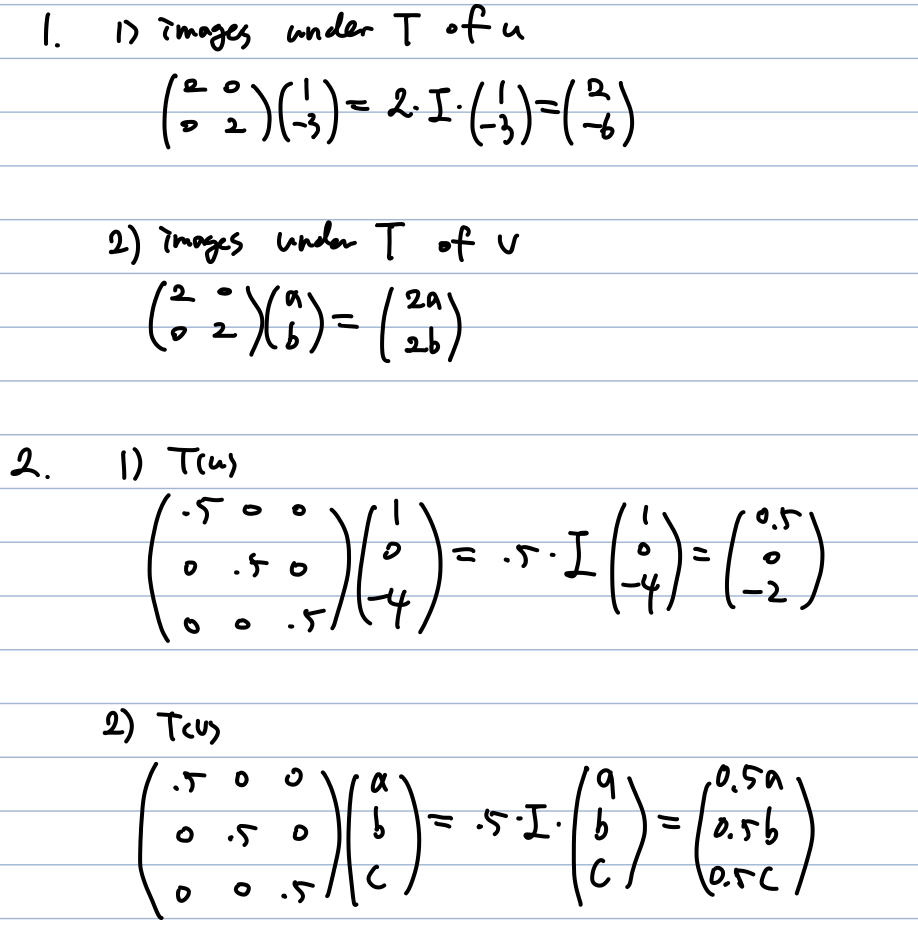
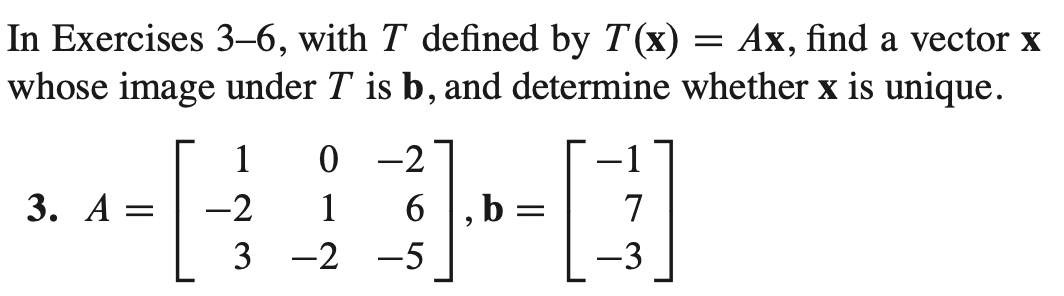
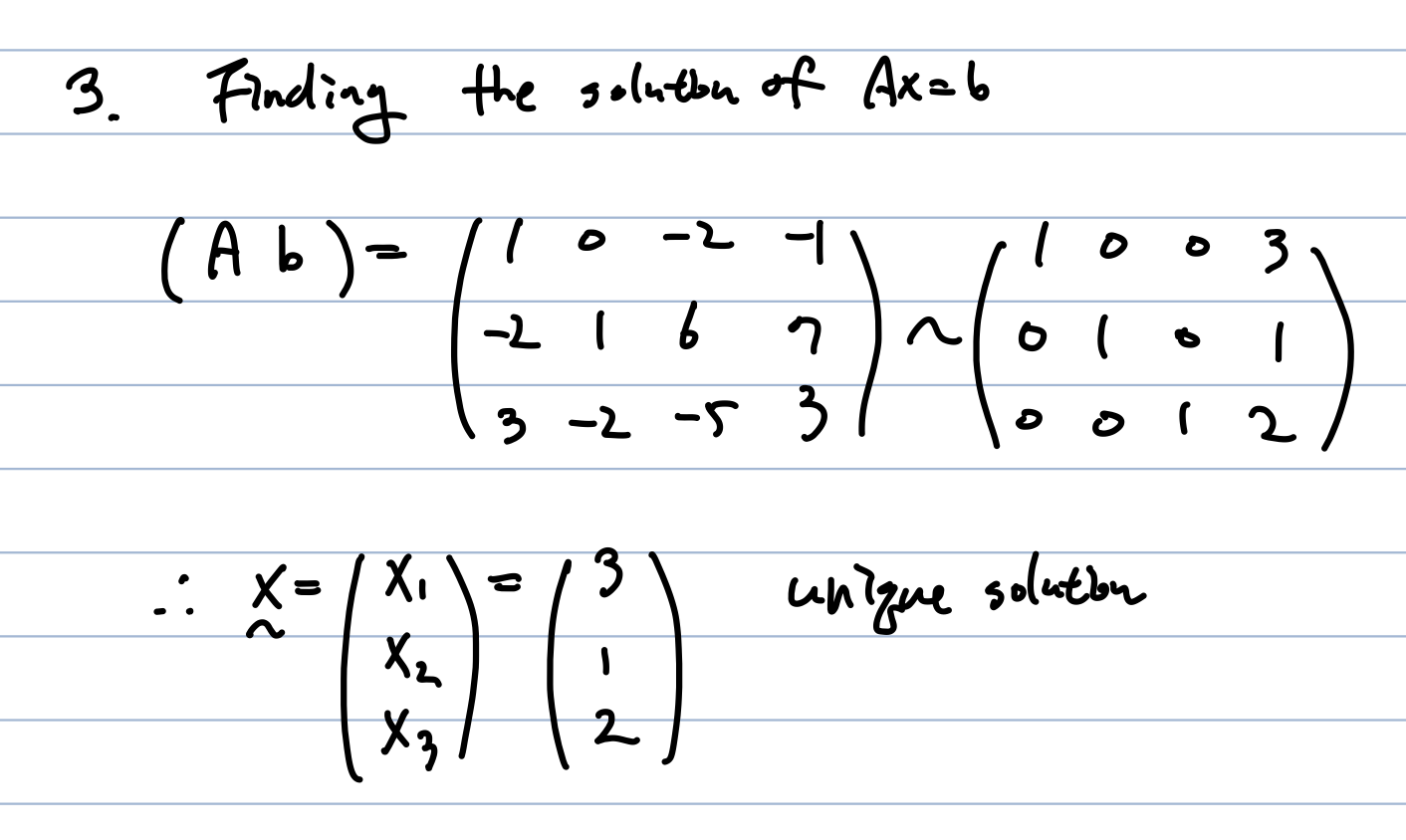
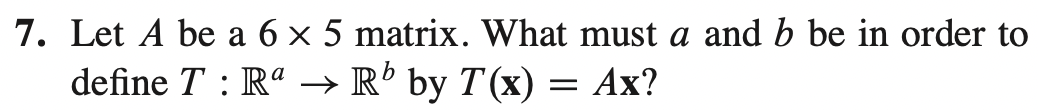
* a = 5, b = 6 이다.
* A와 곱해질 수 있는 벡터는 5차원 벡터 뿐이다. trasnformation의 결과 벡터는 6차원 벡터가 된다.

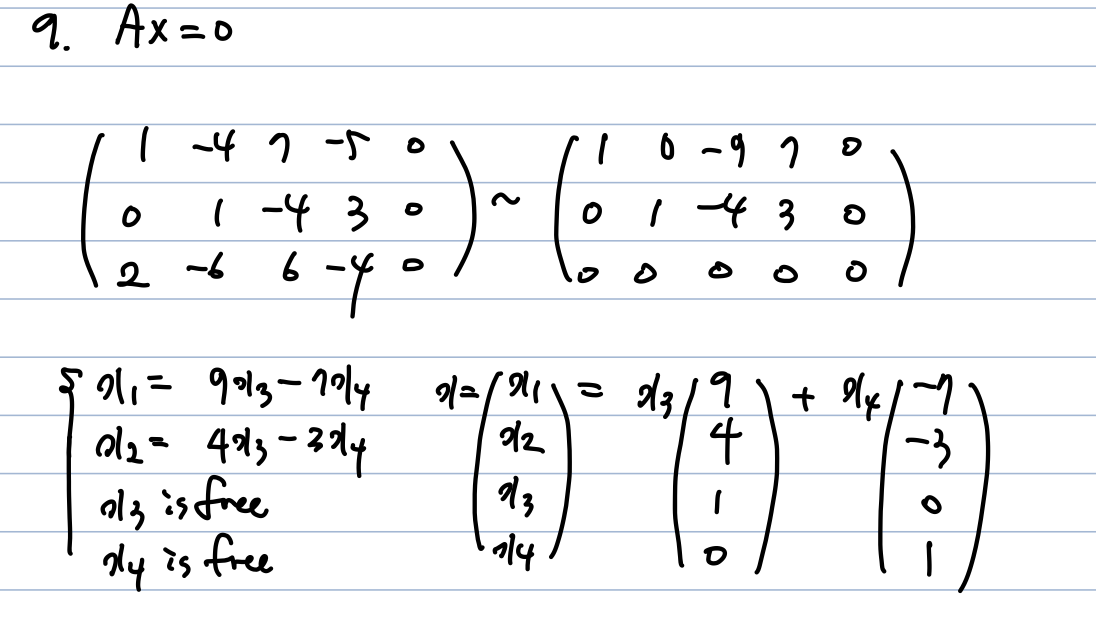


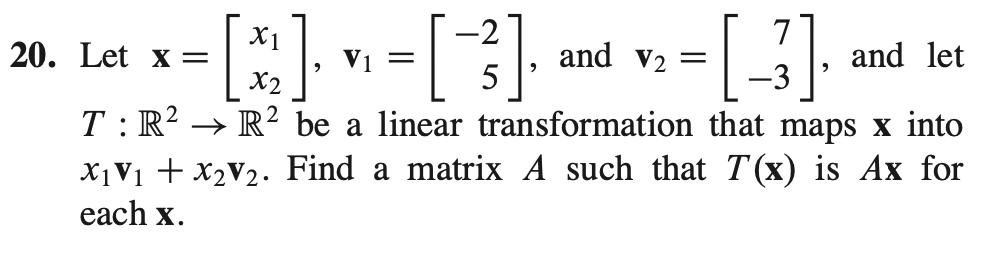
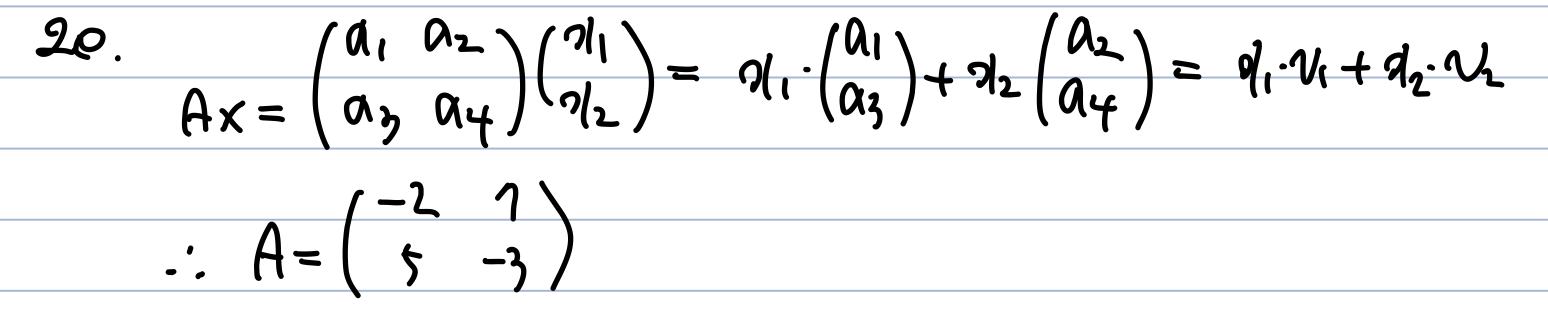

a) 선형성을 유지하는 함수의 일종이다 -> True
b) matrix A에 의해 transform된 벡터는 3차원 실수공간에 속하기 때문에 T의 domain이 3차원 실수공간이라는 명제는 참이다 -> True
c) range는 n차원 실수공간이 된다. -> False
d) 모든 행렬 변환은 선형 변환이다. 하지만 역은 성립하지 않는다. -> False

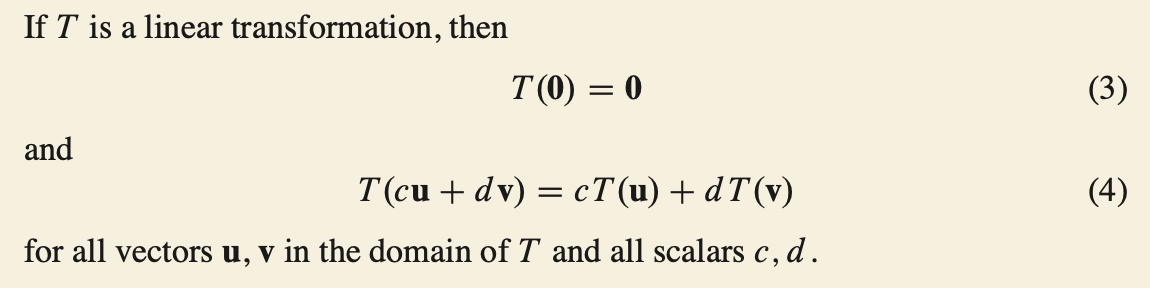
e) True

a) True
b) matrix A가 m x n 크기를 가질 때, A의 column들의 linear combination 결과는 m차원의 벡터이다. 하지만, Ax 의 결과벡터는 n차원 실수공간에 속하므로 명제는 참이 아니다. -> False
c) Is c in the image of T가 맞다. range는 Transformation 되기 전인 domain을 뜻한다. -> False
d) True
e) True



1) T(u), T(v) are linearly independent
* 두 벡터가 선형독립일 경우 T의 image는 span{T(u), T(v)}인 origin, T(u), T(v)를 지나는 plane이 된다.
2) T(u), T(v) are linearly dependent, both not zero
* 두 벡터가 선형종속일 경우 T의 image는 span{T(u), T(v)}인 origin을 지나는 line이 된다.
3) T(u) = T(v) = 0
* Span{T(u), T(v)} = 0

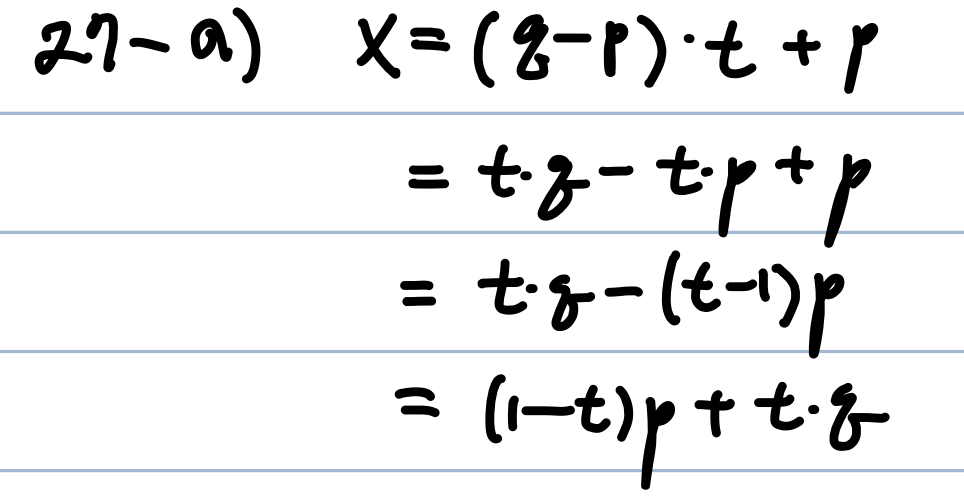
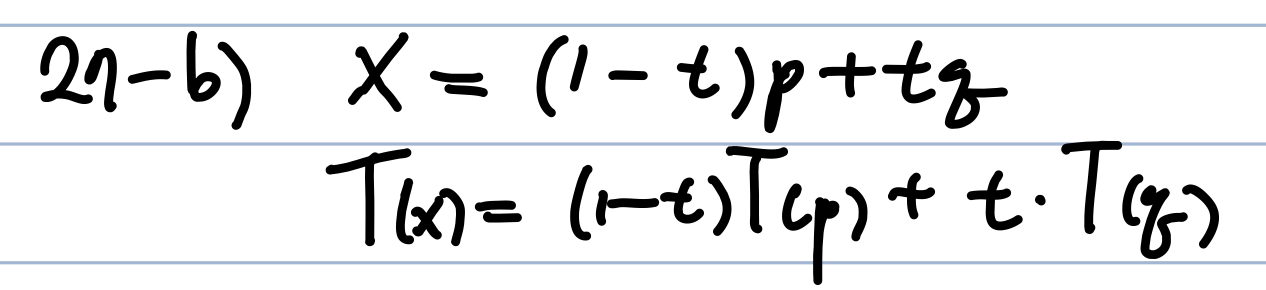
1) T(p) = T(q) = 0
* single point로 mapping됨
2) 다시

* T(p) = T(au + bv) = a*T(u) + b*T(v) 이다.
1) T(u) = T(v) = 0
* single point로 mappling
2) T(u), T(v) are linearly independent
* a = b = 0일 때 0, a = b = 1일 때 T(u) + T(v) 인 line으로 mappling된다.
3) T(u), T(v) are linearly dependent
* degenerated parallelogram(parallelogram or line or point)으로 mapping된다.
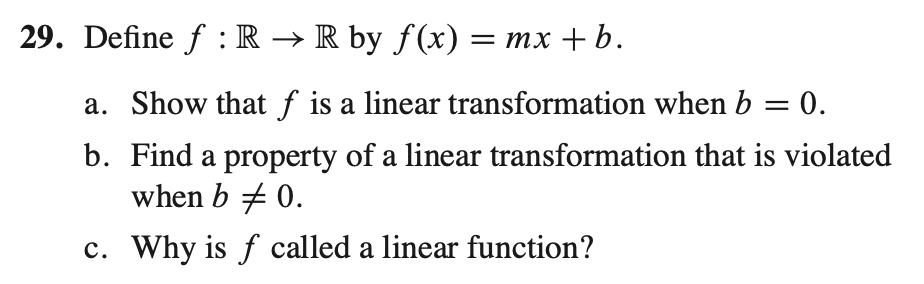
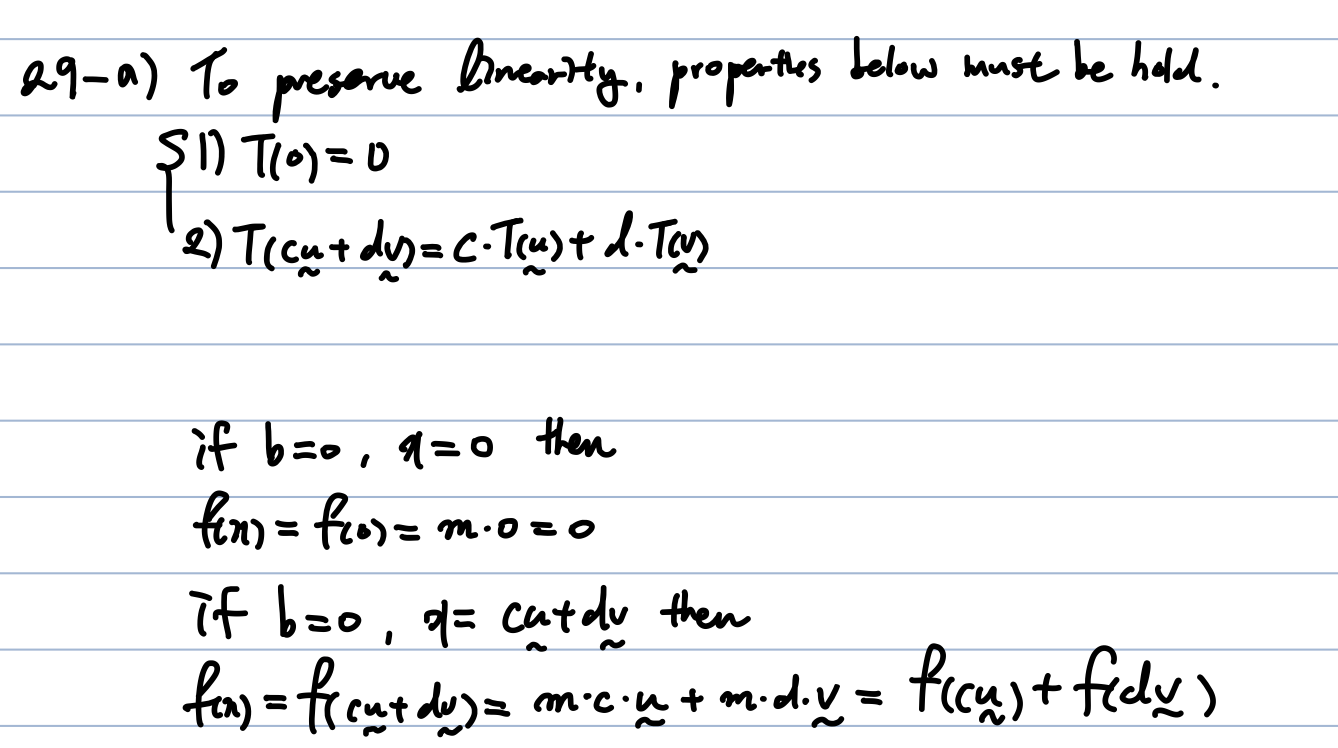
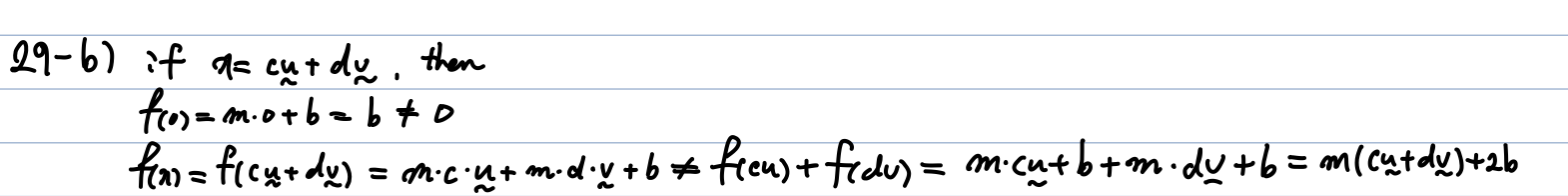
29-c) f가 line 형태이므로 linear function이라고 부른다.

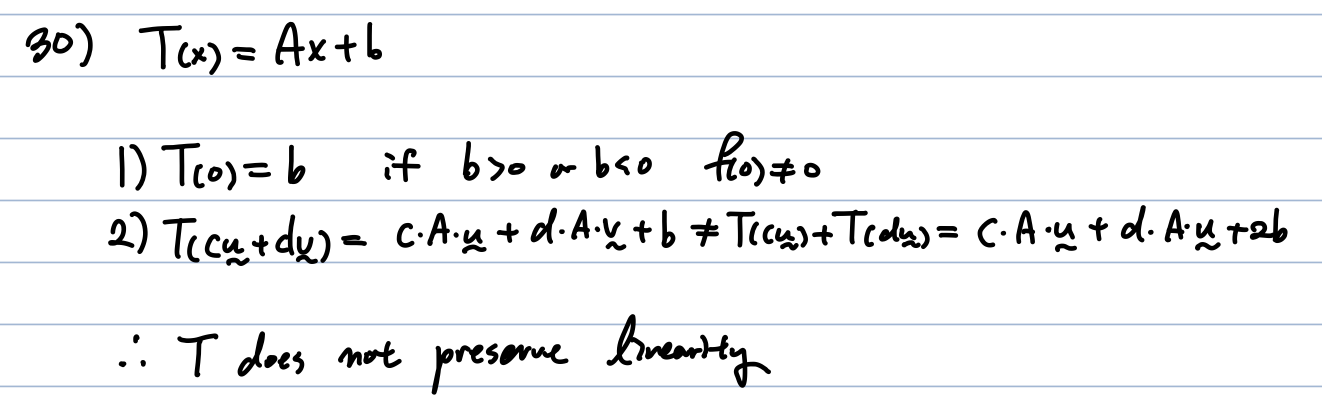

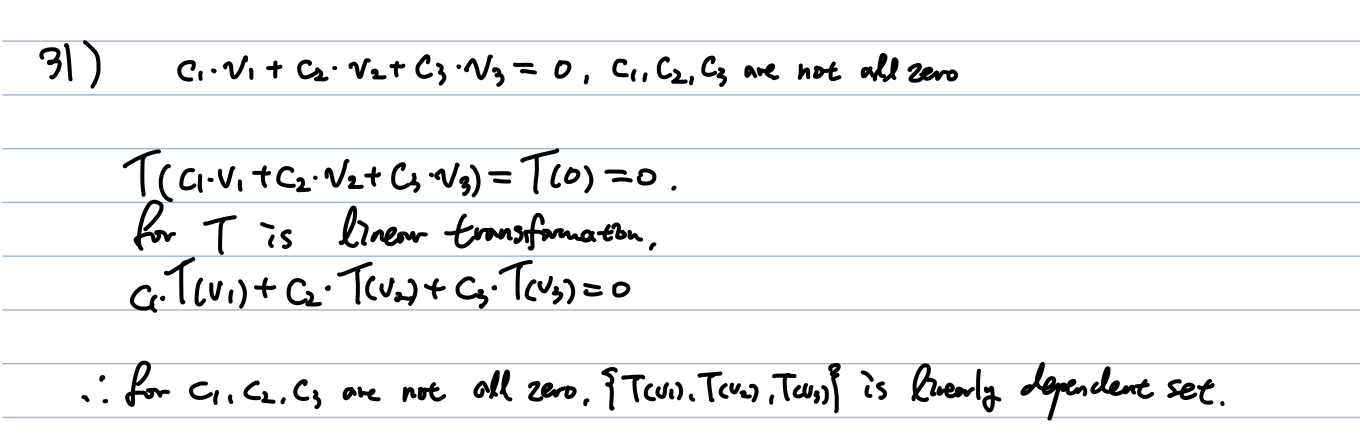


'수학 > Linear Algebra exercise' 카테고리의 다른 글
| 1.7 Linear Independence (0) | 2022.11.13 |
|---|---|
| 1.5 Solution sets of linear systems (0) | 2022.11.12 |
| 1.4 The Matrix Equation exercise (0) | 2022.11.11 |
| 1.2 Row Reduction and Echelon form Exercise (0) | 2022.02.15 |



