

1) non-trivial solution in homogeneous system

2) trivial solution in homogeneous system


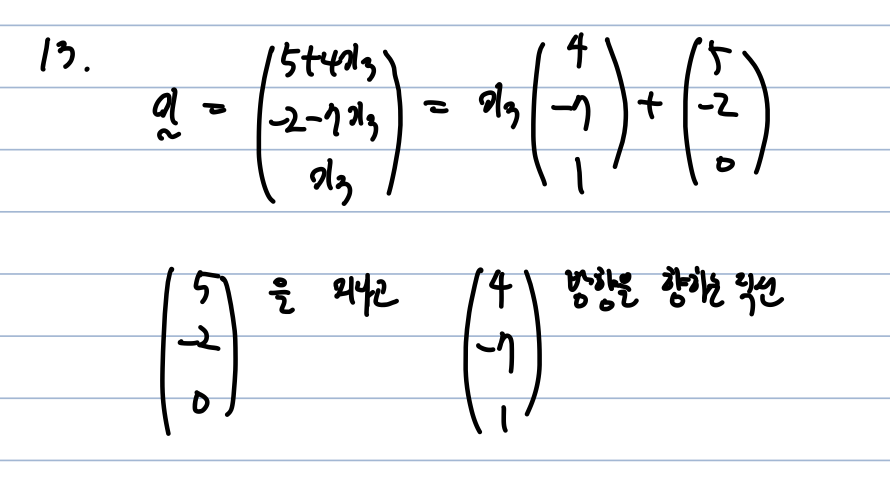



a) homogeneous equation은 trivial solution(zero vector) or non-trivial solution(infinitely many solutions) 만 존재한다. inconsistent할 수가 없다 -> True
b) row reduction을 시행해봐야 알 수 있다. explicit하지 않다 -> False
c) 최소 한 개 이상의 free variable이 존재하면, infinitely many solution set을 갖기 때문에 non-trivial solution이다 -> False
d) 거꾸로 됐다. p를 지나고, vector v와 평행한 line을 뜻한다. -> False
e) non-homogeneous equation의 solution 이 없을 수 있다. Ap = b가 성립할 경우만 statement가 참이 된다. -> False


a) nontrivial solution이라고 해서 x의 모든 entry가 non-zero인 것은 아니다. all-zero만 아니면 된다 -> False
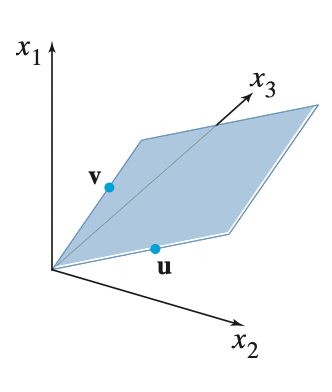
b) 위 그림 참조
c) zero vector가 solution이면 A0 = b = 0 이다. -> True
d) True
e) non-homogeneous system의 solution set을 통해 homogeneous system의 solution set을 구하는 것은 가능하지만 반대는 불가능하다 -> False


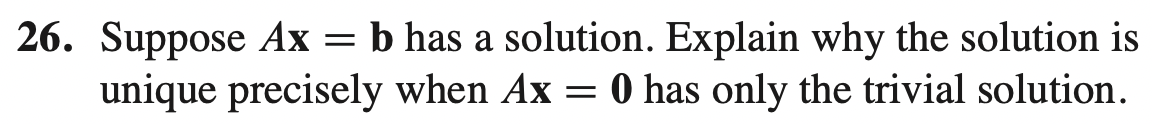
* 이번 단원에서 살펴본 바와 같이 Ax = b 의 solution은 p + v가 되고, 이 때 v는 Ax=0의 solution이다.
* 만약 Ax = 0이 trivial solution을 가지면 x = v = 0이 된다.
* 따라서 Ax = b의 solution은 p + 0 = p 가 되는데, 이 때문에 Ax = b는 unique solution을 가지게 된다.

* solution set은 $\mathbb R^3$차원의 모든 벡터가 될 수 있기 때문에 infinitely many이고, non-trivial solution이 된다.

* 원점을 지날 수 없다. solution set이 원점을 지나려면 x = 0일 때 A0 = 0 이 되야 한다. 하지만, b는 0이 될 수 없다고 가정했기 때문에 원점을 지날 수 없게 된다.

29-a) 모든 column에 pivot 존재, free variable이 존재하지 않음. -> trivial solution
29-b) theorem 4에 의하면 모든 row에 pivot이 존재하면 0 = x 꼴이 존재하지 않기 때문에 적어도 1개의 solution이 존재하게 된다 -> 모든 b에 대해 at least one solution
31-a) 모든 column에 pivot 존재, free variable이 존재하지 않음. -> trivial solution
31-b) 모든 row에 pivot 존재하지 않음. 0=x꼴이 존재할 수 있음 때문에 no solution일 수도 있음. -> 모든 b에 대해 적어도 하나의 solution 성립 x
32-a) 모든 column에 pivot 존재 x, free variable 2개 존재 -> non-trivial solution
32-b) 모든 row에 pivot 존재함. -> 모든 b에 대해 적어도 하나의 solution 존재




'수학 > Linear Algebra exercise' 카테고리의 다른 글
| 1.8 Introduction to linear transformations (0) | 2022.11.15 |
|---|---|
| 1.7 Linear Independence (0) | 2022.11.13 |
| 1.4 The Matrix Equation exercise (0) | 2022.11.11 |
| 1.2 Row Reduction and Echelon form Exercise (0) | 2022.02.15 |



