방정식을 vector equation, matrix equation으로 표현하기
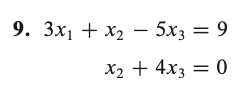
* 위와 같은 방정식이 있을 때
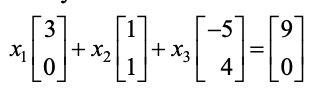
* vector equation은 위와 같이,
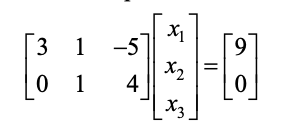
* matrix equation은 위와 같이 표현한다.
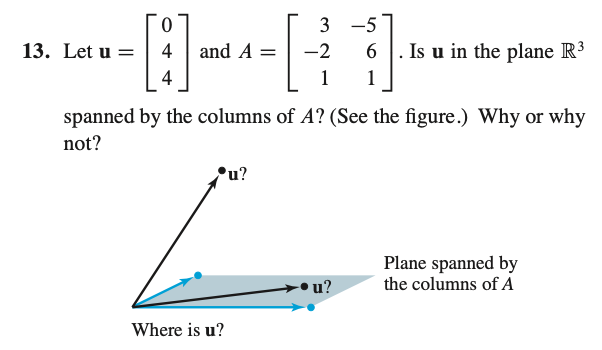
* Ax = u 의 해가 존재한다면 u는 A의 column들에 의해 span되는 것이라고 할 수 있다.
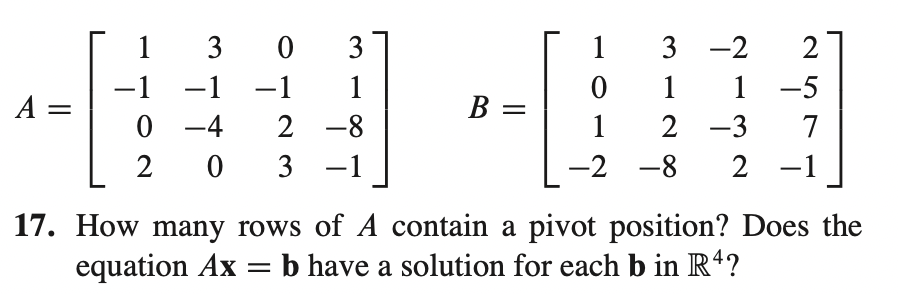
* 만약 Ax = b 의 augmented matrix의 reduced echelon form에서 하나의 row라도 pivot 이 존재하지 않는다면 Ax=b는 solution이 없게 된다.
* $b \in \mathbb R^4$ 이기 때문에 b의 모든 element가 nonzero라고 했을 때 pivot position이 존재하지 않은 row는 0=x꼴이 되기 때문에 해당 system의 solution은 존재하지 않기 때문이다.
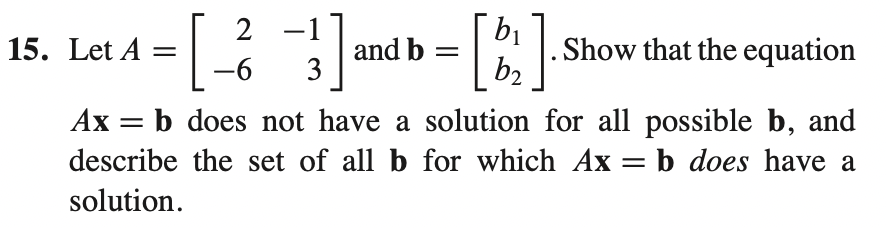

a) Ax = b 는 Matrix equation이라고 부를 수 있다. -> False
b) 적어도 1개 이상의 solution이 존재한다면 consistent하고, A의 linear combination으로 벡터 b를 표현 가능하다. True
c) 주의해야 될 점은 matrix A의 coefficient matrix의 모든 row에 pivot이 존재해야 한다는 점이다. 만약 c번의 예 처럼 [A b]와 같은 augmented matrix가 주어진다면 pivot이 존재한다는 의미가 coefficient matrix에서 논의하던 개념과는 조금 달라진다. -> False
d) Ax 의 결과 벡터는 A의 첫 번째 row와 벡터 x의 내적 값과 같다. -> True
e) True
f) 15번의 예에서 살펴볼 수 있듯이 일부 b에 대해 inconsistent하다면 적어도 1개 이상의 row의 pivot이 없다고 볼 수 있다. -> True

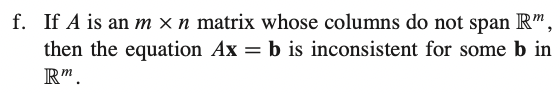
a) matrix equation은 vector equation으로 치환해서 쓰는 것이 가능하다 -> True
b) linear combination은 Ax 와 같이 matrix equation으로 표현 가능하다 -> True
c) True
d) True
e) [0 0 0 0 1]과 같은 row만 존재하지 않으면 consistent하다. -> False
f) 모든 $b \in \mathbb R^m$에 대해 consistent하기 위해서는 matrix A가 $\mathbb R^m$을 span해야 한다. -> True

* 3 x 3 matrix이면서, row reduction을 통해 reduced echelon form 을 생성했을 때 모든 variable이 basic variable이면 $\mathbb R^m$을 span한다.
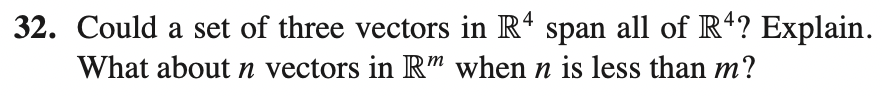
* n이 m보다 작을 경우 m개의 row에 모두 pivot이 존재할 수 없기 때문에 span하는 것이 불가능하다.

* unique solution을 가지려면 free variable이 존재하지 않아야 한다.

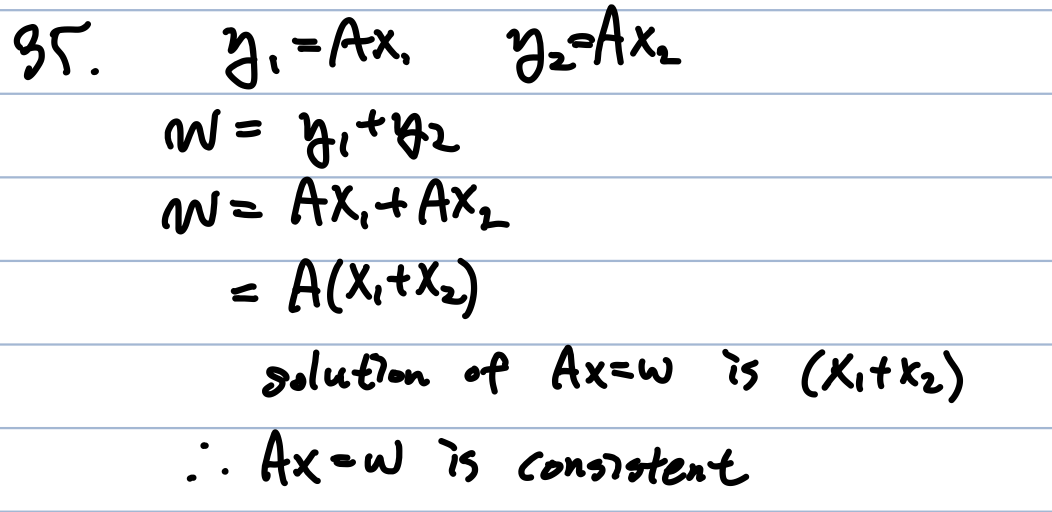
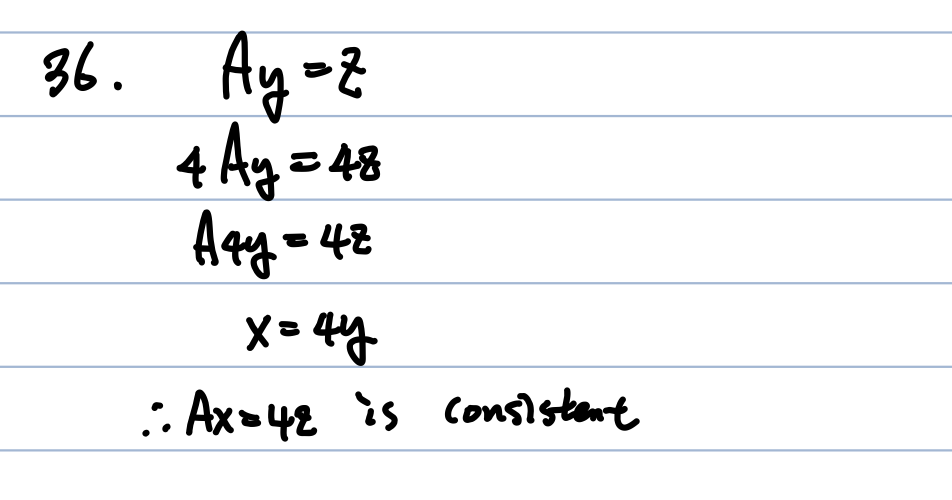
'수학 > Linear Algebra exercise' 카테고리의 다른 글
| 1.8 Introduction to linear transformations (0) | 2022.11.15 |
|---|---|
| 1.7 Linear Independence (0) | 2022.11.13 |
| 1.5 Solution sets of linear systems (0) | 2022.11.12 |
| 1.2 Row Reduction and Echelon form Exercise (0) | 2022.02.15 |



