Intro
* Transformer는 seq2seq의 encoder, decoder를 차용하되, RNN을 제거하고 attention을 사용한 모델이다.
* 처음에 transformer에 대한 개괄적인 설명을 보고 여기서 RNN을 제거하고 attention을 사용한 이유가 뭘까 궁금했다. RNN은 시간 방향으로 하나씩 처리를 하기 때문에 GPU를 활용한 병렬처리가 어렵다. 반면 attention은 time step에 따라 입력 데이터를 처리하지 않고, 입력 데이터를 한 번에 받아(예를 들어 'I have a macbook'이라는 문장을 한 번에 입력받음) 행렬을 사용해 한 번에 처리한다.
* 물론 자세한 구조에 대해 이해하지 않은 상태에서 이런 설명은 와닿지 않겠지만, 정리하자면 'RNN은 시점에 따라 입력을 하나씩 받아 GPU를 사용한 병렬처리가 어렵지만, attention은 행렬 계산을 통해 문장을 처리하기 때문에 GPU를 사용한 병렬 처리가 가능하다'고 생각하면 될 것 같다.
* Transformer의 구조를 그림으로 간략하게 살펴보자.
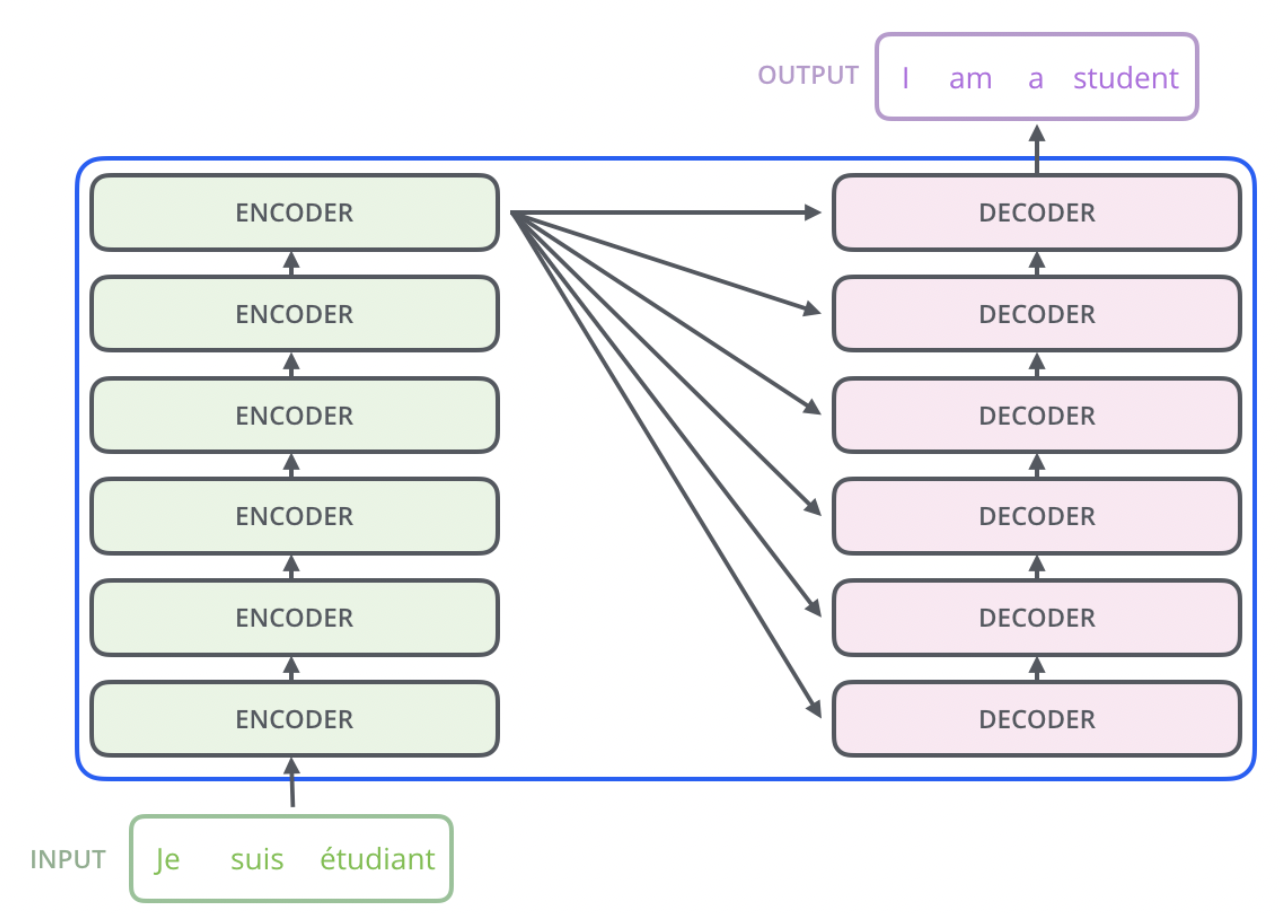
* 논문에서는 encoder 6개, decoder 6개를 사용했다고 했다. 물론 이 encoder, decoder의 개수는 task에 따라 변경할 수 있다.
Positional Encoding
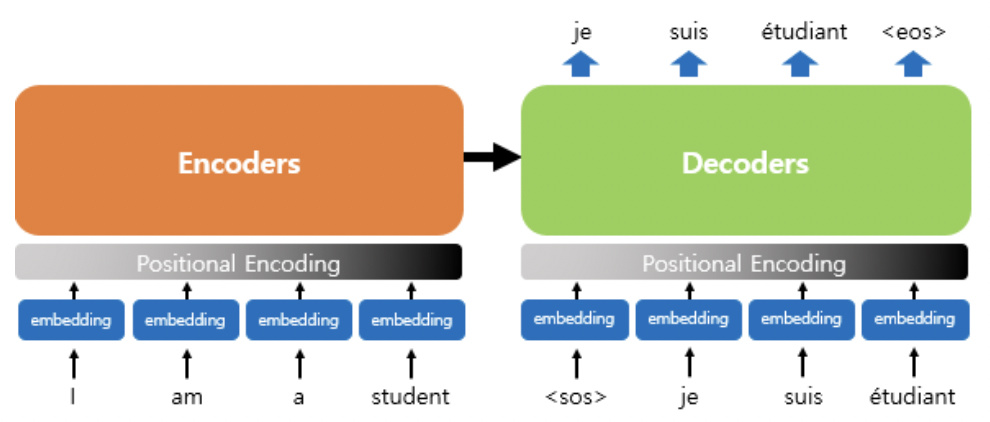
* Transformer는 RNN을 사용하지 않고 입력으로 embedding을 거친 문장 행렬을 한 번에 입력한다고 했다. 그런데 사실 그 사이에는 하나의 계층이 더 들어있는데 바로 Positional Encoding 계층이다.
* positional encoding은 문장에서 단어의 위치값을 더해주는 작업이다. RNN에서 문장에서 단어의 순서는 time step에 따라 구분되는데, 이를 통해 단어가 문장의 어느 위치에 있는지를 구분할 수 있다. 똑같은 작업을 해준다고 생각하면 된다.
* 그런데 이 작업이 왜 필요할까? 우리가 집어넣는 단어 vector는 embedding을 거친 단어 vector이기 때문에 동일한 단어에 대해서는 동일한 vector값을 가진다. 만약 positional encoding을 하지 않는다면 ' The CEO of apple loves to eat some apple at morning' 과 같은 문장에서 회사명을 뜻하는 apple과 과일을 뜻하는 apple이 동일한 단어 vector로 입력될 것이다. 뭔가 좀 문제가 있다. 앞에 있는 apple은 'CEO of' 뒤에 온다는 위치 정보를 통해 회사라는 것을 암시해야 하고, 뒤에 있는 apple은 'eat some' 뒤에 온다는 위치 정보를 통해 과일이라는 것을 암시해야 한다. 이렇게 문장 내에서 단어의 위치 정보를 추가해주는 것은 매우 중요하다.
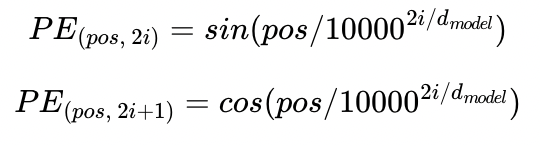
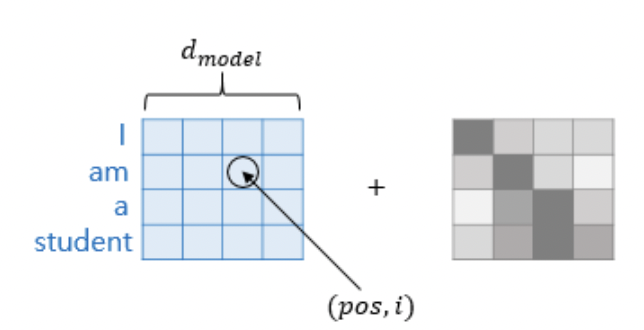
* 다시 돌아와서 Positional Encoding vector는 위와 같은 수식을 통해 계산된다.
* pos는 입력 문장에서의 임베딩 벡터의 위치를 나타낸다(몇 번째 단어인지)
* i 는 임베딩 벡터 내에서의 차원의 index를 나타낸다. 위 matrix에서 보면 몇 번째 열에 속하는지로 해석할 수 있다.
* 이 방식으로 encoder든, decoder든 RNN과 같은 time step에 따른 구분 없이 입력 문장 내의 각 단어들의 위치 정보를 encoding 할 수 있다.
Encoder
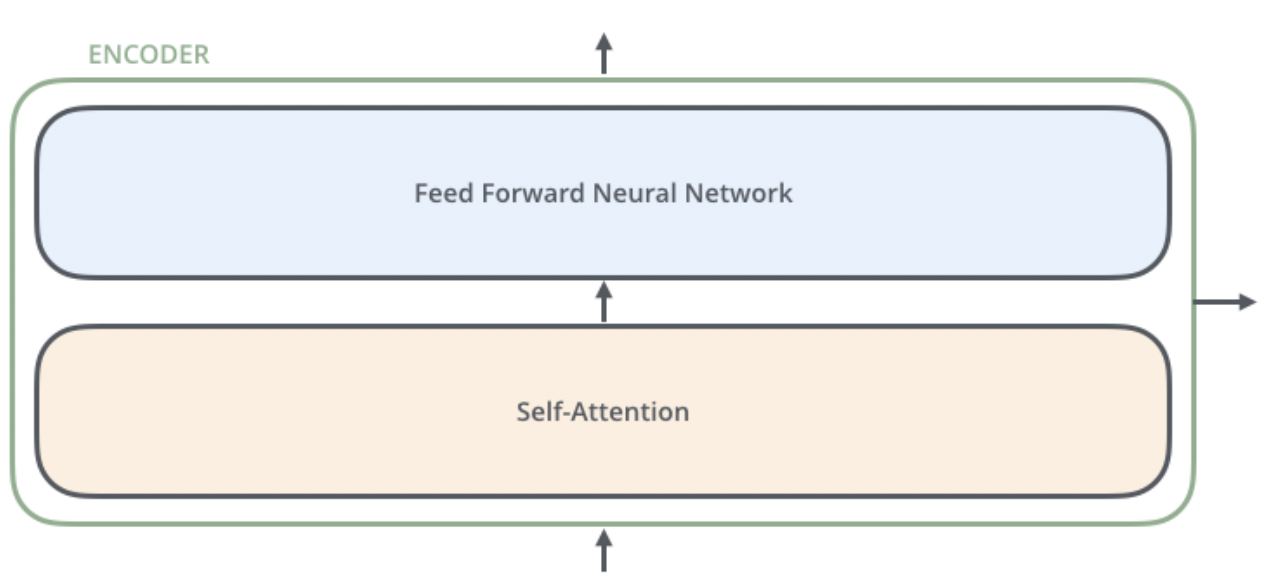
* encoder의 내부를 자세히 들여다보면 위와 같이 self-attention, feed forward neural network 두 개의 계층으로 구성되어 있다.
* feed forward NN은 뒤에 자세히 살펴보겠지만, 한 방향으로 데이터가 전파되는 신경망을 뜻한다. 딱히 어려울 것은 없다. transformer에 대해 이해하고자 하는 정도의 수준이면 이미 알고 있는 내용일 것이다.
* self attention이 조금 생소한데 self attention부터 어떤 구조인지 살펴보자.
self-attention
* self-attention은 단어 벡터가 문장에 어느 부분에 집중하고 있는지에 대한 정보를 추출하는 과정을 뜻한다.
* self-attention을 요약해보자면 다음과 같다.
- 단어 vector를 query vector로 변환해 query vector에 대해 모든 key vector와의 유사도를 구해 softmax로 유사도를 0~1사이의 값으로 정규화한 후 value vector에 정규화된 유사도를 곱해 최종 attention value를 도출한다.
* 여기서 우리가 아직 배우지 않은 것은 Query vector, Key vector, Value vector이다(이하 Q, K, V vector). 이 Q, K, V vector에 대해 자세히 알아보자.
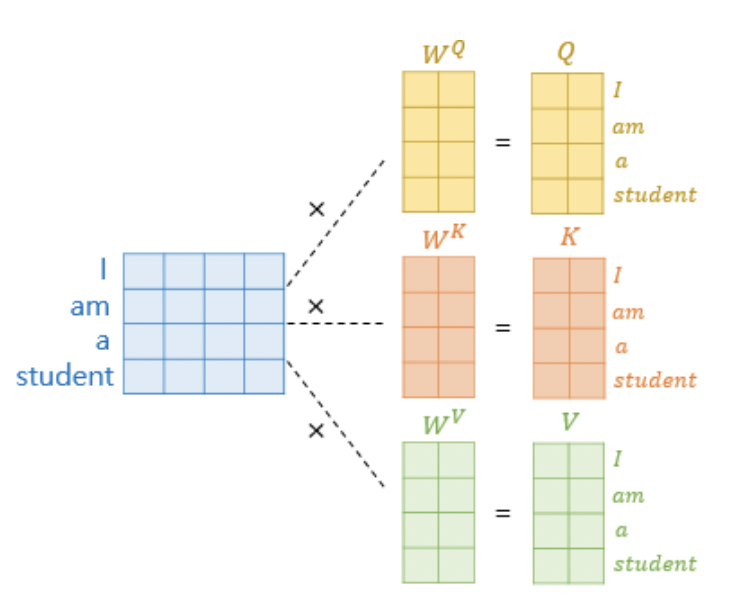
* 관련 문서들을 정독한 결과, vector 단위로 개념을 익힌 뒤 실제 처리 과정에 맞춰 개념을 행렬 단위로 확장하는 것 보다 애초에 행렬 단위에서 개념을 익혀버리는게 낫다고 생각해서 행렬단위 설명을 해보겠다.
* embedding을 통해 도출된 문장 행렬은 각 Q, K, V matrix로 변환되기 위해 $W^Q, W^K, W^V$ 의 가중치 행렬과 곱해진다.
* 여기서 Q, V, K matrix의 각 행벡터의 차원은 문장 행렬의 각 행 벡터의 차원을 뜻하는 d_model을 하이퍼파라미터로 설정하는 num_heads 로 나눈 값으로 설정된다. 예를 들어 d_model이 512이고, $num_heads$가 8이라면 Q, V, K matrix의 각 행벡터 차원은 64가 된다. 이는 추후에 설명할 multi-head attention에서 더 자세히 설명한다.
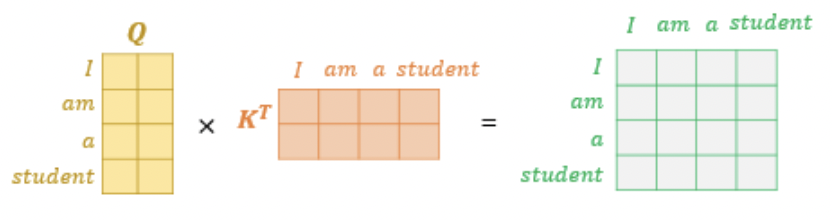
* 이렇게 도출된 Q matrix의 각 행 벡터는 query를 의미한다. Q matrix는 transpose된 K matrix와 곱해져 각 단어들간의 내적을 통해 유사도를 나타내는 matrix가 된다.
* 오른쪽 matrix의 첫 번째 행은 query인 I vector와 key인 I, am, a, student vector들간의 내적을 통해 구한 유사도로 구성되어 있다. 예를 들어 오른쪽 matrix의 첫 번째 행의 첫 번재 원소는 I와 I의 유사도, 두 번째 원소는 I와 am의 유사도를 나타낸다.
* 이렇게 특정 단어 q가 주어졌을 때 해당 단어를 포함한(하지만 I를 나타내는 q vector와 I를 나타내는 k vector는 동일한 벡터가 아니기 때문에 유사도가 1이 안 나옴) 다른 단어 k 와의 유사도를 구함으로서 '특정 단어를 처리할 때 문장의 어느 부분에 집중해야 하는지'를 알 수 있게 된다.
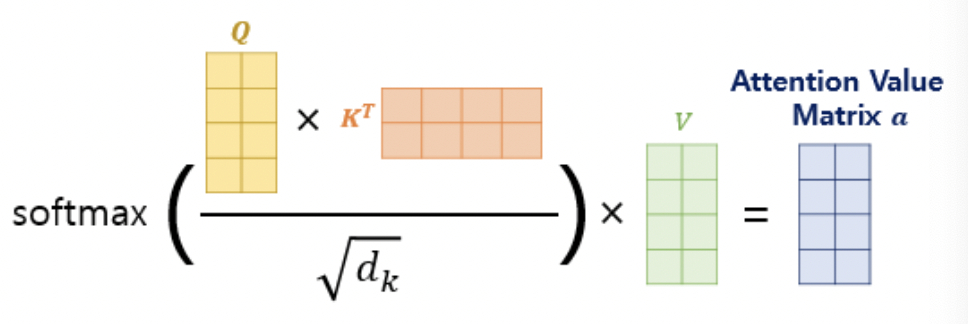
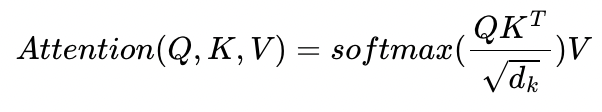
* 그리고 이 attention score를 0~1사이의 값으로 정규화 해주기 위해 $\sqrt{d_k}$ (여기서 $d_k$는 embedding vector의 차원 수)로 나눠주고 softmax를 취해준다.
* softmax를 취해준 0~1사이의 값을 value matrix와 곱해주면 최종적으로 Attention value matrix a가 도출된다.
* 이 attention value matix는 '각 query 단어가 문장의 어느 부분과 관련 되있는지' 에 대한 정보를 담고 있는 vector이다.
* 예를 들어 Attention value matrix의 첫 번째 행은 query 인 ' I '가 문장의 어느 부분과 관련되어 있는지(예를 들어 am과 0.3만큼 관련되어 있고, a와 0.1만큼 관련 되어 있고, student와 0.6만큼 관련되어있다는 등의 정보) 를 나타내는 vector이다.
* 지금까지의 과정을 코드로 구현해보자.
def scaled_dot_product_attention(query, key, value, mask):
# query 크기 : (batch_size, num_heads, query의 문장 길이, d_model/num_heads)
# key 크기 : (batch_size, num_heads, key의 문장 길이, d_model/num_heads)
# value 크기 : (batch_size, num_heads, value의 문장 길이, d_model/num_heads)
# padding_mask : (batch_size, 1, 1, key의 문장 길이)
# Q와 K의 곱. 어텐션 스코어 행렬.
matmul_qk = tf.matmul(query, key, transpose_b=True)
# 스케일링
# dk의 루트값으로 나눠준다.
depth = tf.cast(tf.shape(key)[-1], tf.float32)
logits = matmul_qk / tf.math.sqrt(depth)
# 마스킹. 어텐션 스코어 행렬의 마스킹 할 위치에 매우 작은 음수값을 넣는다.
# 매우 작은 값이므로 소프트맥스 함수를 지나면 행렬의 해당 위치의 값은 0이 된다.
if mask is not None:
logits += (mask * -1e9)
# 소프트맥스 함수는 마지막 차원인 key의 문장 길이 방향으로 수행된다.
# attention weight : (batch_size, num_heads, query의 문장 길이, key의 문장 길이)
attention_weights = tf.nn.softmax(logits, axis=-1)
# output : (batch_size, num_heads, query의 문장 길이, d_model/num_heads)
output = tf.matmul(attention_weights, value)
return output, attention_weights
Padding Mask
def scaled_dot_product_attention(query, key, value, mask):
... 중략 ...
logits += (mask * -1e9) # 어텐션 스코어 행렬인 logits에 mask*-1e9 값을 더해주고 있다.
... 중략 ...* 앞서 구현했던 함수에서 mask라는 parameter를 받아 mask에 매우 작은 수를 곱해서 logits에 최종적으로 더하는 내용이 있었다. 이는 입력 문장에 <pad> 토큰이 있을 때 어텐션에서 제외하기 위한 연산이다.
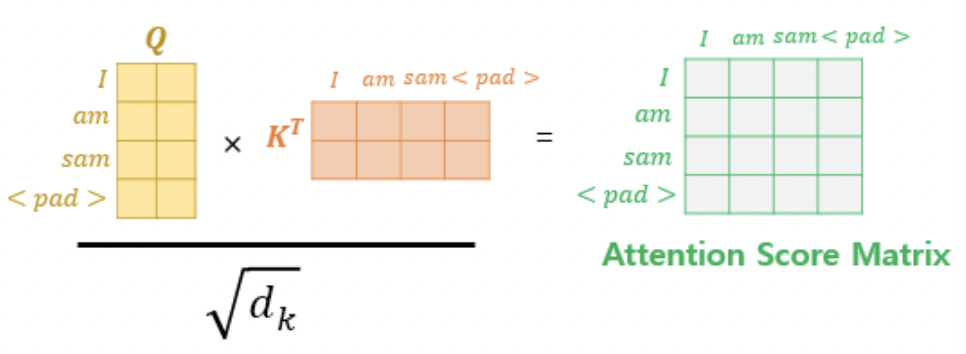
* 입력 문장에 <pad>가 있을 경우 attention score matrix는 오른쪽과 같이 구해지는데, 각 단어들과 <pad>의 유사도는 구할 필요가 없기 때문에 key가 <pad> 일 경우 해당 열을 매우 작은 음수값(ex - -1000000000)마스킹 해준다.
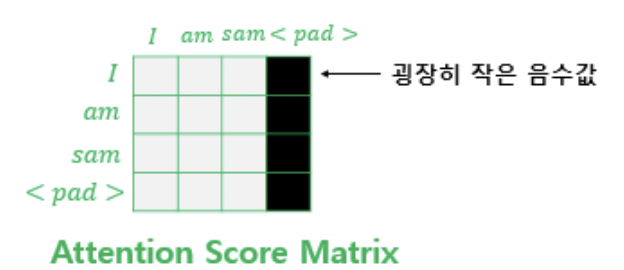
* 이렇게 마스킹 된 열의 값들은 softmax 를 거치며 정규화 되어 0이 된다.
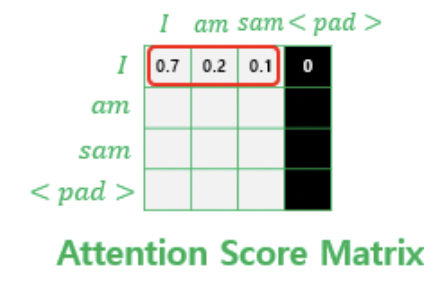
* python으로 구현하면 아래와 같다.
def create_padding_mask(x):
mask = tf.cast(tf.math.equal(x, 0), tf.float32)
# (batch_size, 1, 1, key의 문장 길이)
return mask[:, tf.newaxis, tf.newaxis, :]
print(create_padding_mask(tf.constant([[1, 21, 777, 0, 0]])))
# tf.Tensor([[[[0. 0. 0. 1. 1.]]]], shape=(1, 1, 1, 5), dtype=float32)* 결과 tensor의 1인 부분은 이전에 생성한 scaled_dot_product_attention 함수에 들어가 -1e9가 곱해져 매우 작은 음수가 된다.
Multi-head Attention
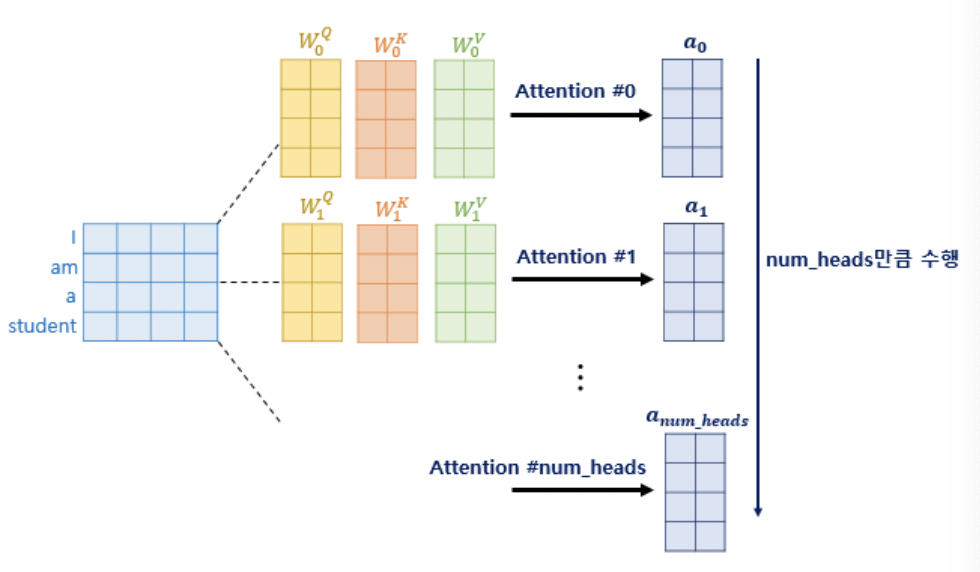
* 앞서 Q, K, V matrix의 각 행벡터의 차원은 d_model / num_heads로 설정한다는 것을 언급한 바 있다.
* 이는 multi-head attention을 위한 처리였고, num_heads의 head는 multi-head attention의 head 개수를 뜻한다.
* 한 번의 attention 처리보다 여러 번의 attention처리를 병렬로 진행하는 것이 더 다양한 시각의 정보를 담을 수 있다. 예를 들어 'the animal didn't cross the road because it was too tired'라는 문장이 주어졌을 떄 query가 ' it '이라면, 첫 번째 attention은 it과 animal의 유사도를 높게 보고, 두 번째 attention은 it과 tired의 유사도를 높게 보는 등 여러 시각에서 다양한 결과를 얻을 수 있게 된다.
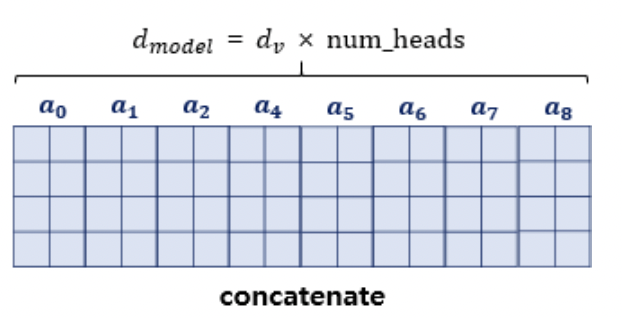
* 이렇게 얻어진 attention value들은 행 방향으로 concatenate된다.
* concatenate된 attention value matrix의 shape은 (seq_len, $d_{model}$) 이다. 이 concatenated matrix는 가중치 행렬 $W^o$와 곱해진다. $W^o$의 shape은 ($d_v$ $\times$ num_heads, $d_{model}$) 이다.
* 결국 concatenated matrix $\times$ $W^o$ = Multi-head attention matrix가 되고, 이 multi-head attention matrix의 shape은 (seq_len, $d_{model}$)이 된다. 이는 입력되었던 문장 행렬의 shape과 동일한 shape이다.
class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, name="multi_head_attention"):
super(MultiHeadAttention, self).__init__(name=name)
self.num_heads = num_heads
self.d_model = d_model
assert d_model % self.num_heads == 0
# d_model을 num_heads로 나눈 값.
# 논문 기준 : 64
self.depth = d_model // self.num_heads
# WQ, WK, WV에 해당하는 밀집층 정의
self.query_dense = tf.keras.layers.Dense(units=d_model)
self.key_dense = tf.keras.layers.Dense(units=d_model)
self.value_dense = tf.keras.layers.Dense(units=d_model)
# WO에 해당하는 밀집층 정의
self.dense = tf.keras.layers.Dense(units=d_model)
# num_heads 개수만큼 q, k, v를 split하는 함수
def split_heads(self, inputs, batch_size):
inputs = tf.reshape(
inputs, shape=(batch_size, -1, self.num_heads, self.depth))
return tf.transpose(inputs, perm=[0, 2, 1, 3])
def call(self, inputs):
query, key, value, mask = inputs['query'], inputs['key'], inputs[
'value'], inputs['mask']
batch_size = tf.shape(query)[0]
# 1. WQ, WK, WV에 해당하는 밀집층 지나기
# q : (batch_size, query의 문장 길이, d_model)
# k : (batch_size, key의 문장 길이, d_model)
# v : (batch_size, value의 문장 길이, d_model)
# 참고) 인코더(k, v)-디코더(q) 어텐션에서는 query 길이와 key, value의 길이는 다를 수 있다.
query = self.query_dense(query)
key = self.key_dense(key)
value = self.value_dense(value)
# 2. 헤드 나누기
# q : (batch_size, num_heads, query의 문장 길이, d_model/num_heads)
# k : (batch_size, num_heads, key의 문장 길이, d_model/num_heads)
# v : (batch_size, num_heads, value의 문장 길이, d_model/num_heads)
query = self.split_heads(query, batch_size)
key = self.split_heads(key, batch_size)
value = self.split_heads(value, batch_size)
# 3. 스케일드 닷 프로덕트 어텐션. 앞서 구현한 함수 사용.
# (batch_size, num_heads, query의 문장 길이, d_model/num_heads)
scaled_attention, _ = scaled_dot_product_attention(query, key, value, mask)
# (batch_size, query의 문장 길이, num_heads, d_model/num_heads)
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3])
# 4. 헤드 연결(concatenate)하기
# (batch_size, query의 문장 길이, d_model)
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model))
# 5. WO에 해당하는 밀집층 지나기
# (batch_size, query의 문장 길이, d_model)
outputs = self.dense(concat_attention)
return outputs
Feed Forward Neural Network
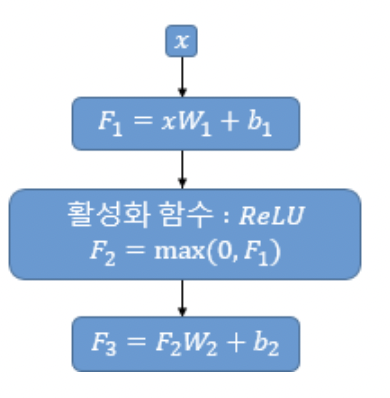
* self-attention의 결과로서 도출됐던 shape이 (seq_len, $d_{model}$)인 multi-head attention matrix는 FFNN에 입력된다.
* $W_1$의 shape은 ($d_{model}, d_{ff}$) 이다.
* $W_2$의 shape은 ($d_{ff}, d_{model}$) 이다.
* $d_{ff}$는 해당 신경망의 은닉층 크기를 의미한다.
* 결국 FFNN을 지난 matrix의 shape은 (seq_len, $d_{model}$)가 되어 최초 입력되었던 문장 행렬과 동일한 shape의 matrix를 출력하게 된다.
Residual connection & Layer normalization
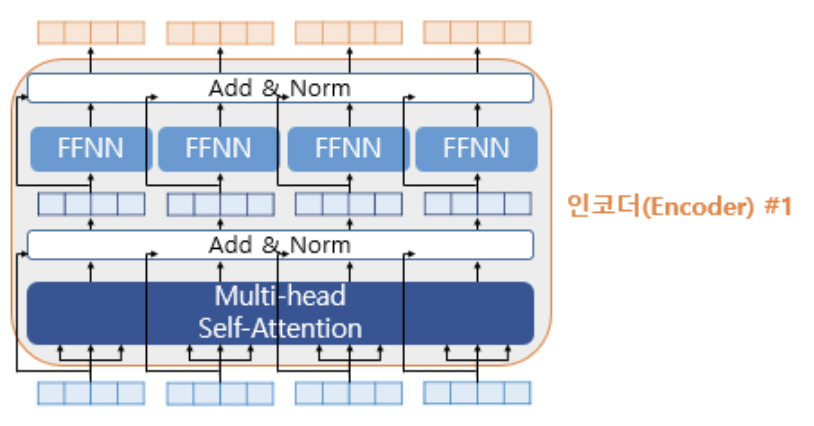
1) Residual Connection
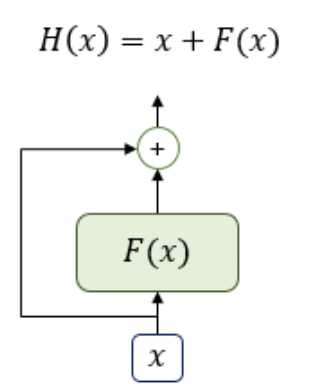
* residual connection은 layer에 입력되는 값을 layer에 통과하는 값에 더해주는 것을 의미한다. 위 그림에서 F(x)은 multi-head self-attention 혹은 FFNN과 같은 sublayer를 의미한다.
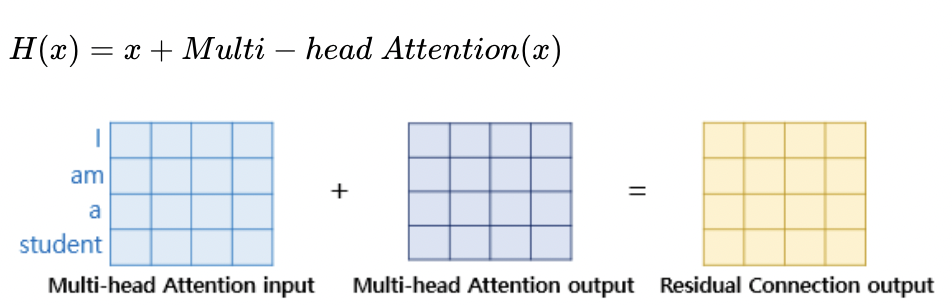
* 만약 F(x)가 multi-head attention이었다면, 계산은 위와 같을 것이다.
2) Layer Normalization
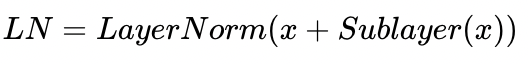
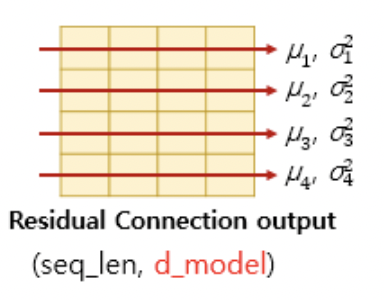
* residual connection을 끝낸 이후에는 layer normalization을 시행한다.
* 먼저 layer normalization 하기 위해서는 데이터의 마지막 차원 방향으로 평균 $\mu$와 분산 $\sigma^2$를 구해 정규화 한다.
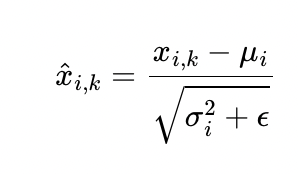
* vector $x_i$의 각 차원을 k라고 했을 때 각 차원 k 값이 위와 같이 되도록 정규화 해준다. $\epsilon$은 분모가 0이 되는 것을 방지하는 아주 작은 수이다.
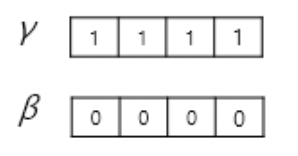
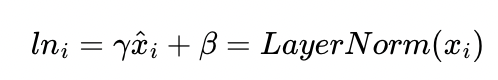
* 그리고 학습 가능한 parameter $\gamma$, $\beta$를 곱해주고 더해준다. $\gamma, \beta$의 차원은 단어 vector의 차원과 동일하다.
Encoder 구현
def encoder_layer(dff, d_model, num_heads, dropout, name="encoder_layer"):
inputs = tf.keras.Input(shape=(None, d_model), name="inputs")
# 인코더는 패딩 마스크 사용
padding_mask = tf.keras.Input(shape=(1, 1, None), name="padding_mask")
# 멀티-헤드 어텐션 (첫번째 서브층 / 셀프 어텐션)
attention = MultiHeadAttention(
d_model, num_heads, name="attention")({
'query': inputs, 'key': inputs, 'value': inputs, # Q = K = V
'mask': padding_mask # 패딩 마스크 사용
})
# 드롭아웃 + 잔차 연결과 층 정규화
attention = tf.keras.layers.Dropout(rate=dropout)(attention)
attention = tf.keras.layers.LayerNormalization(
epsilon=1e-6)(inputs + attention)
# 포지션 와이즈 피드 포워드 신경망 (두번째 서브층)
outputs = tf.keras.layers.Dense(units=dff, activation='relu')(attention)
outputs = tf.keras.layers.Dense(units=d_model)(outputs)
# 드롭아웃 + 잔차 연결과 층 정규화
outputs = tf.keras.layers.Dropout(rate=dropout)(outputs)
outputs = tf.keras.layers.LayerNormalization(
epsilon=1e-6)(attention + outputs)
return tf.keras.Model(
inputs=[inputs, padding_mask], outputs=outputs, name=name)def encoder(vocab_size, num_layers, dff,
d_model, num_heads, dropout,
name="encoder"):
inputs = tf.keras.Input(shape=(None,), name="inputs")
# 인코더는 패딩 마스크 사용
padding_mask = tf.keras.Input(shape=(1, 1, None), name="padding_mask")
# 포지셔널 인코딩 + 드롭아웃
embeddings = tf.keras.layers.Embedding(vocab_size, d_model)(inputs)
embeddings *= tf.math.sqrt(tf.cast(d_model, tf.float32))
embeddings = PositionalEncoding(vocab_size, d_model)(embeddings)
outputs = tf.keras.layers.Dropout(rate=dropout)(embeddings)
# 인코더를 num_layers개 쌓기
for i in range(num_layers):
outputs = encoder_layer(dff=dff, d_model=d_model, num_heads=num_heads,
dropout=dropout, name="encoder_layer_{}".format(i),
)([outputs, padding_mask])
return tf.keras.Model(
inputs=[inputs, padding_mask], outputs=outputs, name=name)Decoder
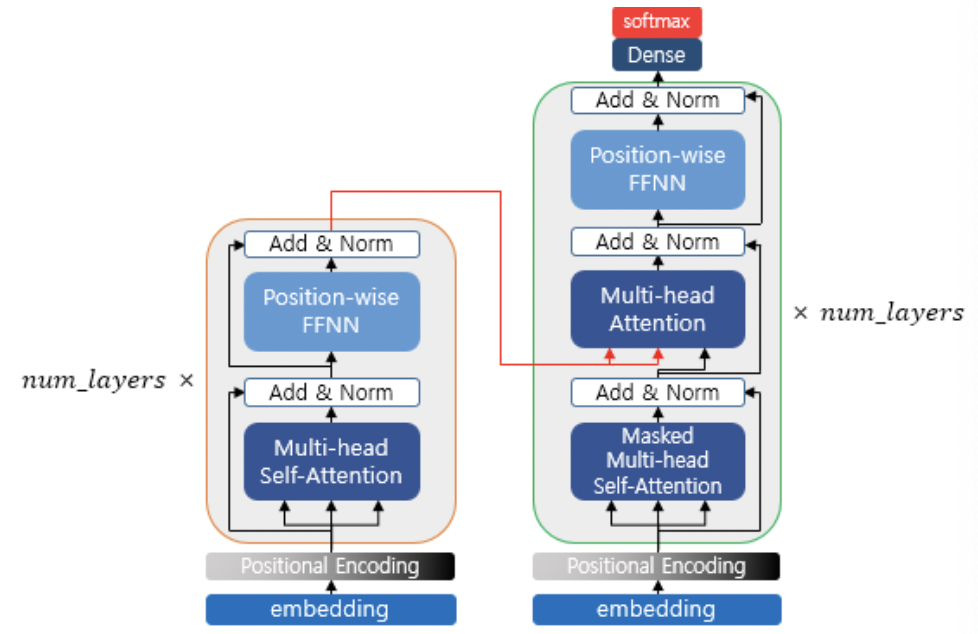
* decoder의 구조는 위와 같다.
self-attention & look-ahead mask
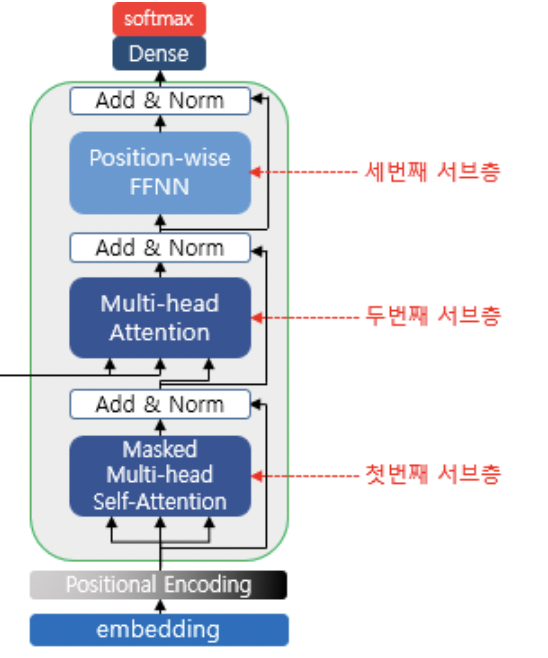
* decoder 또한 마찬가지로 입력은 Embedding을 거치고, positional encoding이 수행된 문장행렬이다.
* 이 때 문장행렬이 들어오기 때문에 입력 단어 처리시 예측해야 할 다음 단어가 decoder에게 그대로 주어지게 된다. 문제집을 푸는데 문제 바로 밑에 정답이 적혀있는 꼴과 같다. 정답 위에 포스트잇을 붙이던지 화이트로 덮던지 해서 정답을 보지 않고 문제를 풀게 해야 한다.
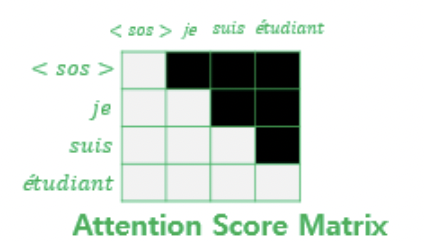
* 유사도를 나타내는 attention score matrix에서 다음 시점의 단어에 대해 위와 같이 마스킹을 함으로서 해당 단어와 이전 단어만 참고할 수 있게 되었다.
* python으로 구현하면 다음과 같다.
def create_look_ahead_mask(x):
seq_len = tf.shape(x)[1]
look_ahead_mask = 1 - tf.linalg.band_part(tf.ones((seq_len, seq_len)), -1, 0)
padding_mask = create_padding_mask(x) # 패딩 마스크도 포함
return tf.maximum(look_ahead_mask, padding_mask)
print(create_look_ahead_mask(tf.constant([[1, 2, 0, 4, 5]])))
# tf.Tensor(
# [[[[0. 1. 1. 1. 1.]
# [0. 0. 1. 1. 1.]
# [0. 0. 1. 1. 1.]
# [0. 0. 1. 0. 1.]
# [0. 0. 1. 0. 0.]]]], shape=(1, 1, 5, 5), dtype=float32)
Encoder-Decoder Attention

* decoder의 두 번째 sub layer를 살펴보자. 이름이 지금까지 봤던 것과 조금 다르다. self가 빠진 것을 볼 수 있다.
* self가 빠진 이유는 key matrix와 value matrix를 encoder의 출력으로부터 생성하기 때문이다. 조금 더 자세히 설명하자면, encoder의 출력은 encoder의 입력과 shape이 같다. 때문에 encoder의 출력에 $W^K, W^V$를 곱해서 key, value matrix를 생성하고, Query matrix만 decoder의 입력에 $W^Q$ matrix를 사용해 도출하는 것이다.
* 이후 multi-head attention을 수행하는 과정은 다른 attention들과 같다.
Dense-Softmax layer
* dense layer는 vocab_size만큼의 unit을 가진 network이다. 이를 통해 $d_{model}$크기의 단어 벡터들이 corpus의 단어 개수 vocab size 크기의 벡터로 변환된다.
* 이후 softmax layer를 거치며 0~1사이의 정규화 된 값을 통해 단어 벡터 다음에 올 단어가 무슨 단어일지를 확률로서 표현한다.
* 말로 주저리주저리 써 놓으니까 이해가 잘 안될 수도 있을 것 같아 아까 사용했던 예시를 다시 가져와보겠다.
* 위 matrix 자료는 우리가 입력을 표현할 때 사용했던 자료이지만, 어짜피 decoder의 출력은 decoder의 입력과 동일한 shape이기 때문에 위 자료를 그냥 decoder의 출력이라고 생각해보자. corpus엔 'I, am, a, student' 4개의 단어밖에 없으므로 vocab_size는 4이다.
* 첫 번째 행은 I 에 해당하는 vector이다. 이 vector는 dense layer를 지나며 vocab size만큼의 vector로 변환된다. 그리고 softmax layer를 지나면서 각 단어 index에 다음 단어로 올 확률이 적힌 vector로 변환된다. 만약 정상적으로 훈련되었다면 I 다음에는 am이 와야 할 것이다. softmax layer를 지난 vector는 [0, 0.9, 0.02, 0.08]과 같은 형태가 될 것이다.
Decoder 구현
def decoder_layer(dff, d_model, num_heads, dropout, name="decoder_layer"):
inputs = tf.keras.Input(shape=(None, d_model), name="inputs")
enc_outputs = tf.keras.Input(shape=(None, d_model), name="encoder_outputs")
# 룩어헤드 마스크(첫번째 서브층)
look_ahead_mask = tf.keras.Input(
shape=(1, None, None), name="look_ahead_mask")
# 패딩 마스크(두번째 서브층)
padding_mask = tf.keras.Input(shape=(1, 1, None), name='padding_mask')
# 멀티-헤드 어텐션 (첫번째 서브층 / 마스크드 셀프 어텐션)
attention1 = MultiHeadAttention(
d_model, num_heads, name="attention_1")(inputs={
'query': inputs, 'key': inputs, 'value': inputs, # Q = K = V
'mask': look_ahead_mask # 룩어헤드 마스크
})
# 잔차 연결과 층 정규화
attention1 = tf.keras.layers.LayerNormalization(
epsilon=1e-6)(attention1 + inputs)
# 멀티-헤드 어텐션 (두번째 서브층 / 디코더-인코더 어텐션)
attention2 = MultiHeadAttention(
d_model, num_heads, name="attention_2")(inputs={
'query': attention1, 'key': enc_outputs, 'value': enc_outputs, # Q != K = V
'mask': padding_mask # 패딩 마스크
})
# 드롭아웃 + 잔차 연결과 층 정규화
attention2 = tf.keras.layers.Dropout(rate=dropout)(attention2)
attention2 = tf.keras.layers.LayerNormalization(
epsilon=1e-6)(attention2 + attention1)
# 포지션 와이즈 피드 포워드 신경망 (세번째 서브층)
outputs = tf.keras.layers.Dense(units=dff, activation='relu')(attention2)
outputs = tf.keras.layers.Dense(units=d_model)(outputs)
# 드롭아웃 + 잔차 연결과 층 정규화
outputs = tf.keras.layers.Dropout(rate=dropout)(outputs)
outputs = tf.keras.layers.LayerNormalization(
epsilon=1e-6)(outputs + attention2)
return tf.keras.Model(
inputs=[inputs, enc_outputs, look_ahead_mask, padding_mask],
outputs=outputs,
name=name)
Decoder 쌓기
def decoder(vocab_size, num_layers, dff,
d_model, num_heads, dropout,
name='decoder'):
inputs = tf.keras.Input(shape=(None,), name='inputs')
enc_outputs = tf.keras.Input(shape=(None, d_model), name='encoder_outputs')
# 디코더는 룩어헤드 마스크(첫번째 서브층)와 패딩 마스크(두번째 서브층) 둘 다 사용.
look_ahead_mask = tf.keras.Input(
shape=(1, None, None), name='look_ahead_mask')
padding_mask = tf.keras.Input(shape=(1, 1, None), name='padding_mask')
# 포지셔널 인코딩 + 드롭아웃
embeddings = tf.keras.layers.Embedding(vocab_size, d_model)(inputs)
embeddings *= tf.math.sqrt(tf.cast(d_model, tf.float32))
embeddings = PositionalEncoding(vocab_size, d_model)(embeddings)
outputs = tf.keras.layers.Dropout(rate=dropout)(embeddings)
# 디코더를 num_layers개 쌓기
for i in range(num_layers):
outputs = decoder_layer(dff=dff, d_model=d_model, num_heads=num_heads,
dropout=dropout, name='decoder_layer_{}'.format(i),
)(inputs=[outputs, enc_outputs, look_ahead_mask, padding_mask])
return tf.keras.Model(
inputs=[inputs, enc_outputs, look_ahead_mask, padding_mask],
outputs=outputs,
name=name)
Transformer 구현하기
def transformer(vocab_size, num_layers, dff,
d_model, num_heads, dropout,
name="transformer"):
# 인코더의 입력
inputs = tf.keras.Input(shape=(None,), name="inputs")
# 디코더의 입력
dec_inputs = tf.keras.Input(shape=(None,), name="dec_inputs")
# 인코더의 패딩 마스크
enc_padding_mask = tf.keras.layers.Lambda(
create_padding_mask, output_shape=(1, 1, None),
name='enc_padding_mask')(inputs)
# 디코더의 룩어헤드 마스크(첫번째 서브층)
look_ahead_mask = tf.keras.layers.Lambda(
create_look_ahead_mask, output_shape=(1, None, None),
name='look_ahead_mask')(dec_inputs)
# 디코더의 패딩 마스크(두번째 서브층)
dec_padding_mask = tf.keras.layers.Lambda(
create_padding_mask, output_shape=(1, 1, None),
name='dec_padding_mask')(inputs)
# 인코더의 출력은 enc_outputs. 디코더로 전달된다.
enc_outputs = encoder(vocab_size=vocab_size, num_layers=num_layers, dff=dff,
d_model=d_model, num_heads=num_heads, dropout=dropout,
)(inputs=[inputs, enc_padding_mask]) # 인코더의 입력은 입력 문장과 패딩 마스크
# 디코더의 출력은 dec_outputs. 출력층으로 전달된다.
dec_outputs = decoder(vocab_size=vocab_size, num_layers=num_layers, dff=dff,
d_model=d_model, num_heads=num_heads, dropout=dropout,
)(inputs=[dec_inputs, enc_outputs, look_ahead_mask, dec_padding_mask])
# 다음 단어 예측을 위한 출력층
outputs = tf.keras.layers.Dense(units=vocab_size, name="outputs")(dec_outputs)
return tf.keras.Model(inputs=[inputs, dec_inputs], outputs=outputs, name=name)
하이퍼파라미터 정하기
small_transformer = transformer(
vocab_size = 9000,
num_layers = 4,
dff = 512,
d_model = 128,
num_heads = 4,
dropout = 0.3,
name="small_transformer")
tf.keras.utils.plot_model(
small_transformer, to_file='small_transformer.png', show_shapes=True)
손실함수정의
def loss_function(y_true, y_pred):
y_true = tf.reshape(y_true, shape=(-1, MAX_LENGTH - 1))
loss = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')(y_true, y_pred)
mask = tf.cast(tf.not_equal(y_true, 0), tf.float32)
loss = tf.multiply(loss, mask)
return tf.reduce_mean(loss)
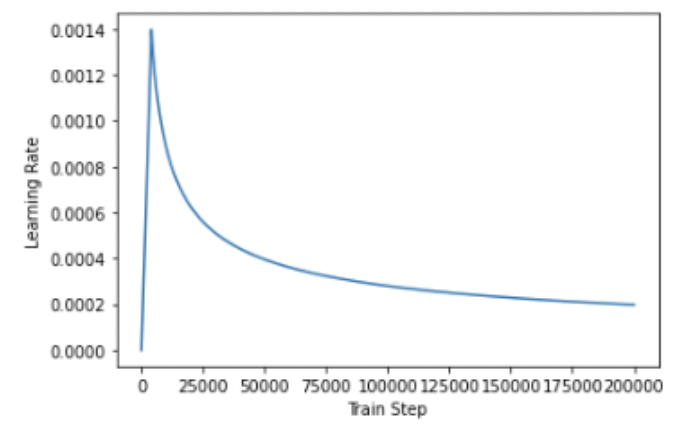
학습률
class CustomSchedule(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, d_model, warmup_steps=4000):
super(CustomSchedule, self).__init__()
self.d_model = d_model
self.d_model = tf.cast(self.d_model, tf.float32)
self.warmup_steps = warmup_steps
def __call__(self, step):
arg1 = tf.math.rsqrt(step)
arg2 = step * (self.warmup_steps**-1.5)
return tf.math.rsqrt(self.d_model) * tf.math.minimum(arg1, arg2)
1) 트랜스포머(Transformer)
* 이번 챕터는 앞서 설명한 어텐션 메커니즘 챕터에 대한 사전 이해가 필요합니다. 트랜스포머(Transformer)는 2017년 구글이 발표한 논문인
wikidocs.net
https://nlpinkorean.github.io/illustrated-transformer/
The Illustrated Transformer
저번 글에서 다뤘던 attention seq2seq 모델에 이어, attention 을 활용한 또 다른 모델인 Transformer 모델에 대해 얘기해보려 합니다. 2017 NIPS에서 Google이 소개했던 Transformer는 NLP 학계에서 정말 큰 주목을
nlpinkorean.github.io
'Deep Learning > 자연어처리' 카테고리의 다른 글
| BERT(Bidirectional Encoder Representations form Transformers) (0) | 2022.02.20 |
|---|---|
| 다양한 단어의 표현방법 (0) | 2022.01.27 |
| Sparse Representation, Dense Representation (0) | 2021.12.27 |
| RNN을 이용한 디코더-인코더 - Seq2Seq (0) | 2021.12.23 |
| 글자 단위 RNN(Char RNN) (0) | 2021.12.18 |



