Bag of Words
* Bag of words는 단어의 순서를 고려하지 않고 출현 빈도에만 집중하는 텍스트 데이터의 수치화 표현 방법이다.
* 각 단어에 index를 부여하고 index 크기 만큼의 vector에 index별 출현 빈도를 표기한 것이 BoW이다.
BoW 만드는 과정
1) 각 단어에 고유한 정수 index 부여
2) 각 index의 위치에 단어 토큰의 등장 횟수를 기록한 벡터를 만듦
from konlpy.tag import Okt
okt = Okt()
def build_bag_of_words(document):
# 온점 제거 및 document 형태소 단위로 분리(list를 return)
document = document.replace('.', '')
tokenized_document = okt.morphs(document)
# 각 단어에 고유 index 부여
word_to_index = {}
# BoW - 단어의 등장 횟수를 기록한 vector
bow = []
for word in tokenized_document:
if word not in word_to_index.keys():
word_to_index[word] = len(word_to_index)
# BoW의 마지막 위치에 1을 삽입(default value = 1)
bow.insert(len(word_to_index) - 1, 1)
else:
# 재등장하는 단어의 인덱스
index = word_to_index.get(word)
# 재등장한 단어는 해당하는 인덱스의 위치에 1을 더한다.
bow[index] = bow[index] + 1
return word_to_index, bow
doc1 = "정부가 발표하는 물가상승률과 소비자가 느끼는 물가상승률은 다르다."
vocab, bow = build_bag_of_words(doc1)
print('vocabulary :', vocab)
print('bag of words vector :', bow)
# vocabulary : {'소비자': 0, '는': 1, '주로': 2, '소비': 3, '하는': 4, '상품': 5, '을': 6, '기준': 7, '으로': 8, '물가상승률': 9, '느낀다': 10}
# bag of words vector : [1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1]* 문서에서 단어별 등장한 횟수를 수치화하기 때문에 문서가 어떤 성격을 띠고 있는지 확인하고 분류하는 작업에 주로 쓰인다. 예를 들어 '달리기', '체력, '근력' 등과 같은 단어가 많이 나오면 체육 관련 문서로 분류할 수 있다.
* 여러 문서, 예를 들어 doc1, doc2 를 합쳐서 단어 집합을 합친 후에 각 문서별로 단어들의 등장 빈도를 나타내는 BoW를 구하는 것도 가능하다. 이러한 처리는 이제 살펴볼 DTM을 생성할 때 사용된다.
문서 단어 행렬(Document-Term Matrix, DTM)
* 여러 개의 BoW vector를 결합한 것을 DTM이라고 한다.
* 예를 들어 아래와 같은 문서 4개가 있다고 해보자.
문서1 : 먹고 싶은 사과
문서2 : 먹고 싶은 바나나
문서3 : 길고 노란 바나나 바나나
문서4 : 저는 과일이 좋아요
* 각 문서를 띄어쓰기를 기준으로 단어 토큰화를 진행한다면 다음과 같다.
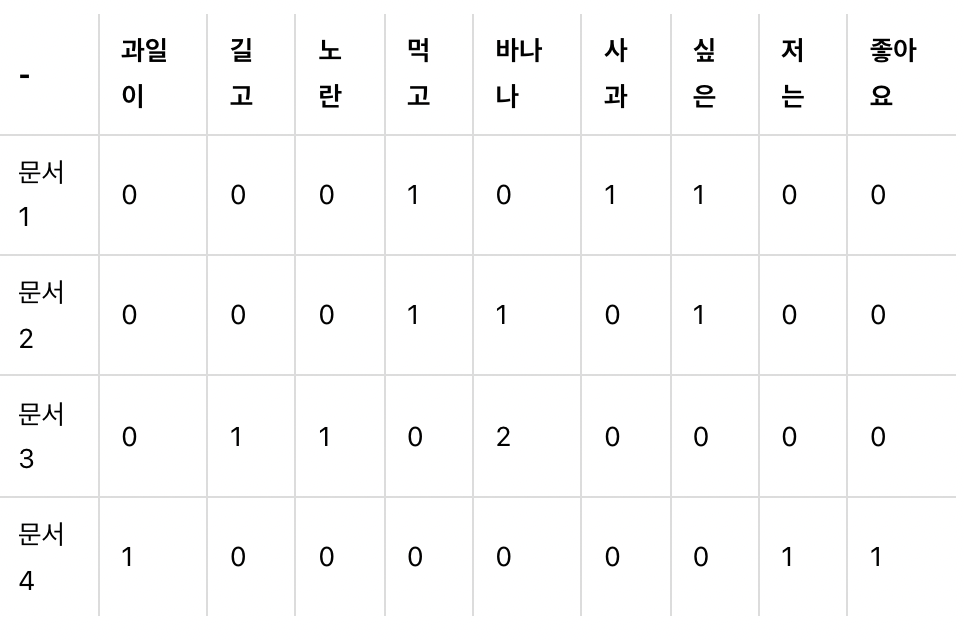
DTM의 한계
1) Sparse Representation
* DTM은 값의 대부분이 0인 sparse matrix이기 때문에 단어집합이 커질수록 많은 양의 저장공간과 높은 계산 복잡도를 요구한다.
* 그래도 조금이나마 한계를 극복하고자 한다면, 구두점, 빈도수가 낮은 단어, 불용어 제거, 어간이나 표제어 추출 등을 통해 단어를 정규화하는 것이 좋을 것이다.
2) 단순 빈도 수 기반 접근
* DTM은 단순히 각 문서의 빈도수를 나타낸 행렬이기 때문에 문서간의 유사도를 비교하고자 할 때 문제가 생긴다. 예를 들어 영어 문서들간의 유사도를 비교하고자 한다고 가정해보자. 불용어인 the와 같은 단어는 모든 문서에 빈번하게 등장할 것이고 이에 따라 모든 문서들이 유사하다(실제로는 아님에도 불구하고)고 결론 지을 수 있는 위험이 존재한다. 이를 해결하기 위해 각 단어에 가중치를 부여하는 방식을 사용할 수 있는데 다음에 살펴볼 TF-IDF이다.
TF-IDF(Term Frequency-Inverse Document Frequency)
* TF-IDF는 DTM의 각 단어들마다 가중치를 부여하는 방식이다.
* 모든 문서에서 자주 등장하는 단어는 낮은 중요도를, 특정 문서에서만 자주 등장하는 단어(해당 문서의 성격을 나타내기 때문에)들은 높은 중요도를 부여한다.
* TF-IDF는 주로 문서의 유사도를 구하거나, 검색 시스템에서 검색 결과의 중요도를 정하거나, 문서 내에서 특정 단어의 중요도를 구하는 작업 등에 쓰일 수 있다.
* 만약 문서를 d, 단어를 t, 문서의 총 개수를 n이라고 한다면 tf, df, idf는 다음과 같다.
1) tf(d, t)
- 특정 문서 d에서 특정 단어 t의 등장 횟수
2) df(t)
- 특정 단어 t가 등장한 문서의 수
3) idf(d, t)
$idf(d, t) = log( {n \over 1+df(t)} )$
- df(t)에 반비례하는 수
- 분모에 log를 취해주는 이유는 문서의 개수 n이 커질수록 기하급수적으로 IDF값이 커지는 것을 막기 위함이다. 또한 희귀 단어들이 등장한 문서의 수 n은 매우 적을텐데, 이 때문에 희귀 단어들이 다른 단어들보다 과도한 가중치를 받는 것을 막기 위해 값을 조정해주기 위함도 있다.
- log 안의 식에서 분모에 1을 더해주는 이유는 특정 단어가 전체 문서 중 어느 문서에도 등장하지 않을 경우($df(t) = 0$) 0으로 나눠지는 것을 방지하기 위해서이다.
TF-IDF 구하기

* 앞서 살펴본 문서 1 ~ 4 의 TF-IDF를 구해보자. 일단 DTM은 우리가 구하려는 TF와 동일하다. 그렇다면 구해야 할 것은 DF와 IDF 뿐이다. IDF에서 사용되는 log는 보통 자연로그이다. 자연로그를 사용해서 IDF를 구해보자.

* 이 IDF값을 DTM의 각 원소에 적용하면 다음과 같은 결과를 얻을 수 있다.

'Deep Learning > 자연어처리' 카테고리의 다른 글
| BERT(Bidirectional Encoder Representations form Transformers) (0) | 2022.02.20 |
|---|---|
| Transformer (0) | 2022.02.20 |
| Sparse Representation, Dense Representation (0) | 2021.12.27 |
| RNN을 이용한 디코더-인코더 - Seq2Seq (0) | 2021.12.23 |
| 글자 단위 RNN(Char RNN) (0) | 2021.12.18 |



