Q-value iteration Algorithm
* 이전 포스팅에서 설명한 최적의 state value를 구하는 알고리즘은 agent의 최적의 policy를 알려주지는 않는다. state value는 상태 s에서의 최적 가치(최적 기대 보상)만을 나타내고, 어떤 action을 선택하는 것이 최적인지에 대해서는 다루지 않기 때문이다.
* Bellman은 추가적으로 state-action 쌍의 최적 value를 추정할 수 있는 알고리즘을 발견했고 이를 Q-value algorithm이라고 한다.
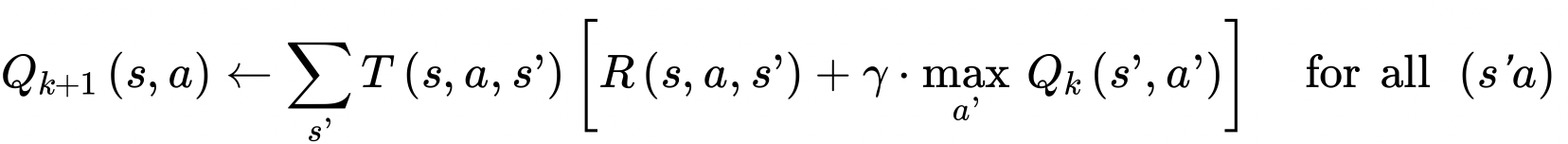
* state value 쌍에 대한 최적의 가치인 Q(s,a)는 agent가 state s에 도달해서 action a를 선택한 후 이 행동의 결과를 얻기 전에 평균적으로 기대할 수 있는(결과를 얻기 전이므로 이전 time step의 Q-value를 활용) 할인된 미래 보상의 합이라고 할 수 있다. 여기서 한 가지 가정은 agent가 이 action a 이후에 최적으로 행동할 것이라는 것이다.
* 먼저 최초 Q value는 모두 0으로 초기화 되고, Q-value iteration algorithm을 통해 update된다.
* 최적의 Q- value를 구하고 나면, agent가 state s에 도달했을 때 가장 높은 Q-value를 가진 action을 선택하면 되기 때문에 최선의 정책 $\pi^* (s)$를 정의하는 것이 가능해진다.
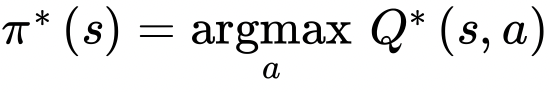
* 이제 Q-value iteration algorithm을 정의해보자.
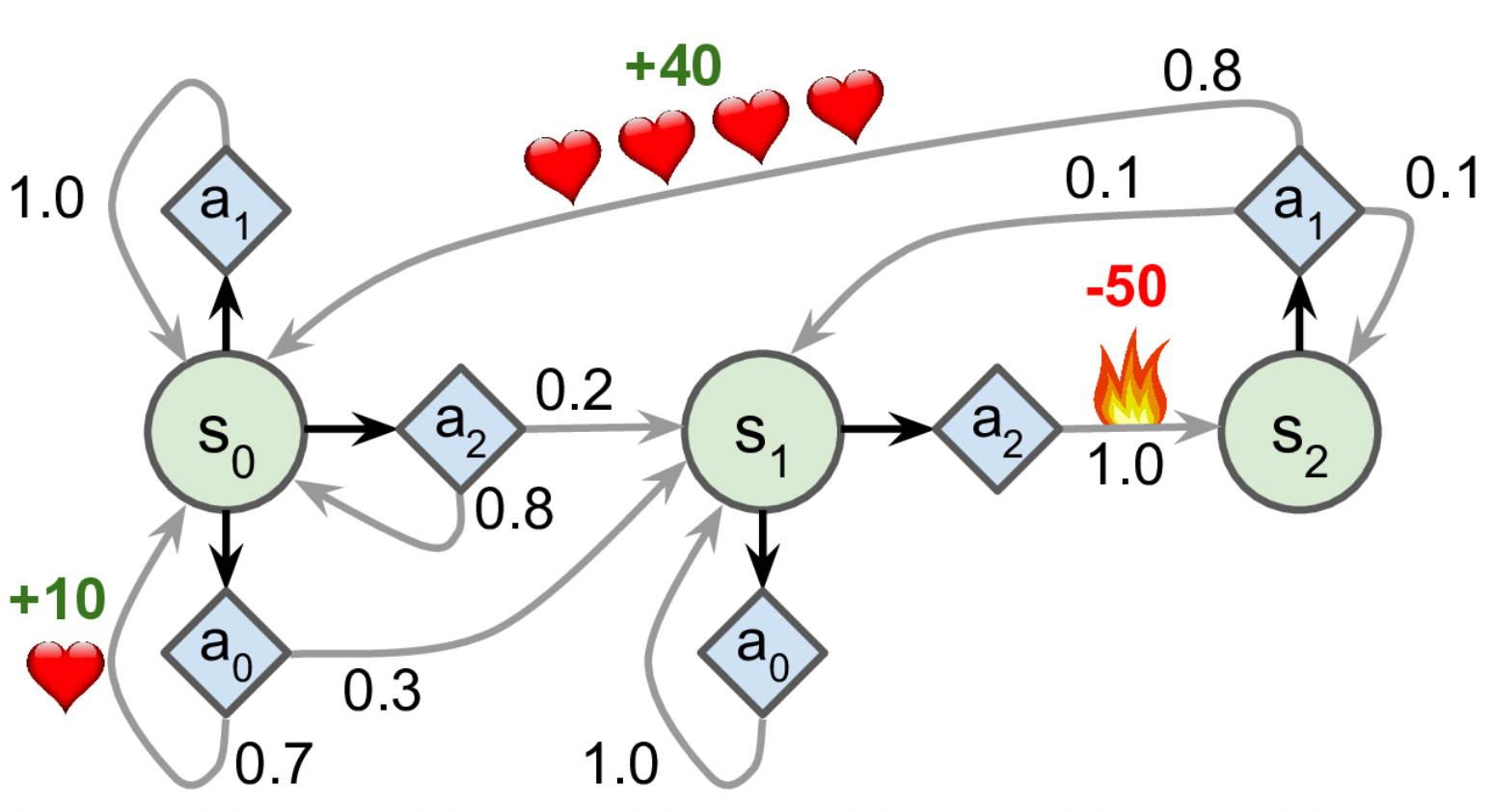
#Markov Decision Process define
transition_probabilities = [ # shape=[s, a, s']
[[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
[[0.0, 1.0, 0.0], None, [0.0, 0.0, 1.0]],
[None, [0.8, 0.1, 0.1], None]]
rewards = [ # shape=[s, a, s']
[[+10, 0, 0], [0, 0, 0], [0, 0, 0]],
[[0, 0, 0], [0, 0, 0], [0, 0, -50]],
[[0, 0, 0], [+40, 0, 0], [0, 0, 0]]]
possible_actions = [[0, 1, 2], [0, 2], [1]]* 먼저 Markov Decision Process를 정의했다.
* transition_probabilities는 shape = [s, a, s']의 규칙을 따르고 있다. 예를 들어 action $a_1$을 플레이한 후 $s_2$에서 $s_0$으로 전이할 확률을 알기 위해서는 transition_probabilities[2][1][0]을 참고한다. reward도 동일하다.
Q_values = np.full((3, 3), -np.inf) # -np.inf for impossible actions
for state, actions in enumerate(possible_actions):
Q_values[state, actions] = 0.0 # for all possible actions
Q_values
# array([[ 0., 0., 0.],
# [ 0., -inf, 0.],
# [-inf, 0., -inf]])* 모든 가능한 action에 대해서는 0으로 초기화 하고 불가능한 action에 대해서는 $-\infty$로 초기화 한다.
* Q_values의 각 원소는 Q_values[s,a]를 나타낸다. state 2의 경우 가능한 action이 action 1밖에 없으므로 [-inf, 0, -inf]형태를 띤다.
gamma = 0.90 # the discount factor
history1 = []
for iteration in range(50):
Q_prev = Q_values.copy()
history1.append(Q_prev)
for s in range(3):
for a in possible_actions[s]:
Q_values[s, a] = np.sum([
transition_probabilities[s][a][sp] # T(s, a, s')
* (rewards[s][a][sp] #R(s, a, s')
+ gamma * np.max(Q_prev[sp])) # gamma * (a'를 최대로 하는 Q_k(s', a'))
for sp in range(3)])
history1 = np.array(history1)
Q_values
# array([[18.91891892, 17.02702702, 13.62162162],
# [ 0. , -inf, -4.87971488],
# [ -inf, 50.13365013, -inf]])* Q-iteration algorithm 수식을 코드로 구현하여 50번 반복한 결과 Q-value가 위와 같이 도출됐다.
* 적절한 정책 $\pi^* (s)$는 state s에 도달하였을 때 할인된 미래 보상의 합이 가장 큰 action을 취하는 것이기 때문에 $s_0$에서는 action $a_0$을, $s_1$에서는 action$a_0$을, $s_1$에서는 action $a_1$을 선택하게 될 것이다.
* 현재 discount factor $\gamma$는 0.90이다. 만약 할인율을 높여(미래 reward의 가치를 더 높게 쳐줌) 0.95로 변경하면 $s_1$에서의 최적 action은 $a_2$가 된다. 즉 불을 통과하여 -50의 reward를 획득하게 되는데, 이는 미래의 행복을 위해 현재의 고통을 감수하려는 성향이 더 커졌기 때문이라고 할 수 있다(정확히는 미래 reward의 가치가 올라갔기 때문에 현재의 음수의 reward도 어느정도 감수하게 되는 것이다).
'Deep Learning > Hands On Machine Learning' 카테고리의 다른 글
| Temporal Difference Learning : TD Learning (0) | 2022.01.08 |
|---|---|
| Markov Decision, State Value Function (0) | 2022.01.08 |
| PG(Policy Gradient) Algorithm (0) | 2022.01.08 |
| 신용할당 문제(Credit Assignment Problem) (0) | 2022.01.08 |
| 강화학습의 신경망 정책 (0) | 2022.01.08 |


