Variational AutoEncoder(변이형 오토인코더)
* variational autoencoder는 여태껏 살펴봤던 autoencoder들과는 조금 다르다. 먼저 probabilistic autoencoder이다. 훈련 과정 뿐만 아니라 테스트 과정에서도 출력이 부분적으로 우연에 의해 결정되기 때문이다(denoise autoencoder가 훈련시에만 gaussian noise 혹은 dropout을 적용하는 것과는 차이가 있다). 두 번째로는 generative autoencoder이다. 훈련 sample에서 생성한 것과 같은 sample을(분포가 같은) 생성할 수 있는 autoencoder이다. 자 이제 variational autoencoder의 구조를 살펴보자.
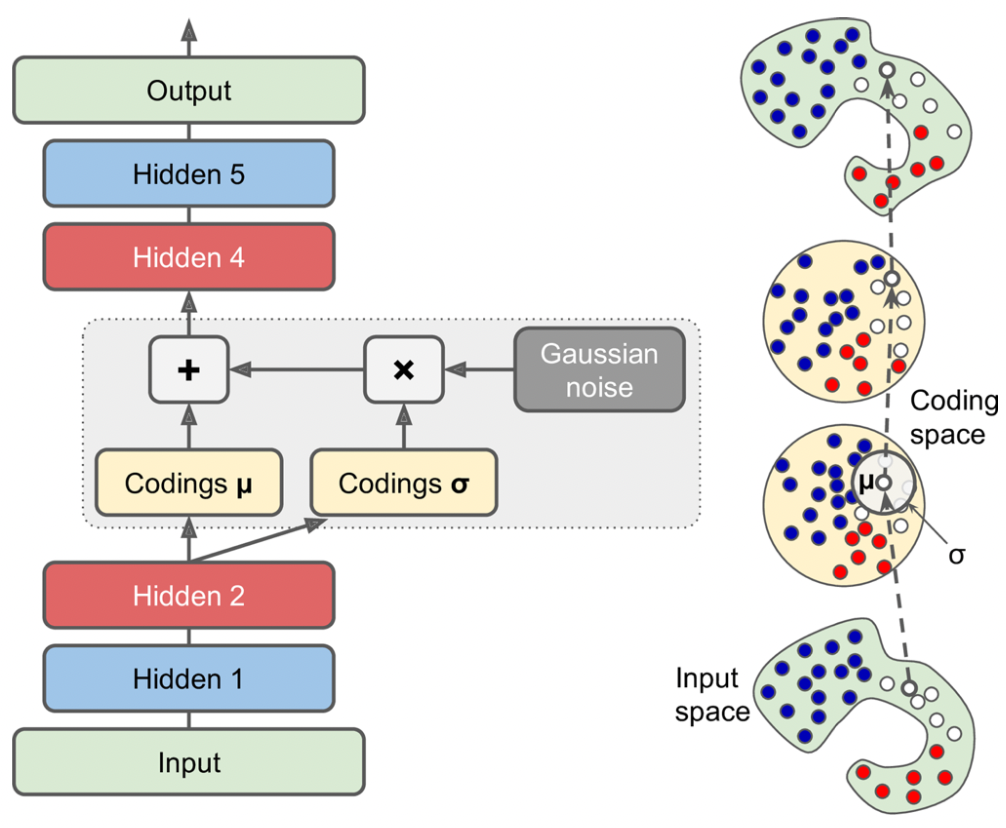
* 구조는 일반적인 autoencoder와 비슷하게 이뤄져 있다. 위 그림을 예로 들자면, 각각 hidden layer가 2개인 encoder, decoder로 구성되어 있다. 하지만, coding을 생성하는 방식이 특이하다. 원래 coding은 encoder의 hidden layer를 거쳐 바로 생성되었지만, variational autoencoder의 coding은 encoder가 생성한 mean coding $\mu$ vector와 standard deviation $\sigma$ vector를 통해 평균이 vector $\mu$이고(coding vector의 각 원소의 평균이 $\mu_1, \mu_2, ... ,\mu_i$), std가 vector $\sigma$인(coding vector의 각 원소의 std가 $\sigma_1, \sigma_2, ... , \sigma_i$) Gaussian distribution에서 random하게 sampling된다. decoder는 이 coding을 가지고 decoding을 시행한다.
* 오른쪽 그림을 보면 input이 아무리 복잡한 distribution을 띠고 있더라도 coding은 Gaussian distribution에서 추출되는 것 처럼 취급할 수 있는데, 이는 loss function이 coding을 gaussian sample처럼 보이도록 coding space(코딩 공간) 혹은 latent space(잠재 공간 )안으로 점진적으로 이동시키기 때문이다.
Cost function
* variational autoencoder의 cost function은 두 부분으로 구성된다.
1) 일반적인 재구성 손실
* 일반적인 재구성 손실을 위해 cross entropy를 사용할 수 있다.
2) 잠재 손실(latent loss)
* 목표 분포와 실제 coding의 분포의 차이를 KL divergence로 계산하는 loss이다. 이는 coding을 Gaussian distribution(normal distribution)에서 sample된 것 같은 coding을 가지도록 autoencoder를 강제하는 역할을 한다.
$L = -\frac{1}{2} \sum_{i=1}^n 1 + log(\sigma_i^2) - \sigma_i^2 - \mu_i^2$
* 위 수식은 잠재 손실 계산식을 간소화 한 식이다. n은 coding의 차원을 나타낸다. 위 수식에서 vector $\sigma$는 표준편차 vector를 나타낸다. 표준편차 vector의 각 원소는 음수가 나올 수 없다. 하지만, 만약 우리가 사용하는 hidden layer의 activation이 sigmoid등이라면 음수가 나올 가능성이 있다. 때문에 음수가 나오면 안된다는 것을 명확히 해주고자 log를 씌워 gamma로 표현하기로 하자.
$L = -\frac{1}{2} \sum_{i=1}^n 1 + log(\gamma_i^2) - \gamma_i^2 - \mu_i^2, \gamma_i = log(\sigma_i^2)$
모델 구현
class Sampling(keras.layers.Layer):
def call(self, inputs):
mean, log_var = inputs #mean vector, log_var vector 받음
return K.random_normal(tf.shape(log_var)) * K.exp(log_var / 2) + mean* Sampling층을 먼저 정의하였다. Sampling층은 $\mu$ vector와 $\sigma$ vector를 입력으로 받는다. 그리고 standard normal distribution에서 $\sigma$ vector와 동일한 크기의 vector를($\mu$ vector의 크기여도 상관 없다) vector를 추출한다. 그 다음 $\sigma$를 만들기 위해 $\gamma$를 생성했던 과정의 역순인 $exp(\gamma / 2)$를 곱한다. 마지막으로 $\mu$를 더해주면 평균이 $\mu$이고 표준편차가 $\sigma$인 normal distribution에서 coding을 sample한 것과 같은 vector가 생성된다.
tf.random.set_seed(42)
np.random.seed(42)
codings_size = 10
inputs = keras.layers.Input(shape=[28, 28])
z = keras.layers.Flatten()(inputs)
z = keras.layers.Dense(150, activation="selu")(z)
z = keras.layers.Dense(100, activation="selu")(z)
codings_mean = keras.layers.Dense(codings_size)(z) # size 10의 mean vector
codings_log_var = keras.layers.Dense(codings_size)(z) # size 10의 std vector
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = keras.models.Model(
inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])
decoder_inputs = keras.layers.Input(shape=[codings_size])
x = keras.layers.Dense(100, activation="selu")(decoder_inputs)
x = keras.layers.Dense(150, activation="selu")(x)
x = keras.layers.Dense(28 * 28, activation="sigmoid")(x)
outputs = keras.layers.Reshape([28, 28])(x)
variational_decoder = keras.models.Model(inputs=[decoder_inputs], outputs=[outputs])
_, _, codings = variational_encoder(inputs) #codings만 사용
reconstructions = variational_decoder(codings)
variational_ae = keras.models.Model(inputs=[inputs], outputs=[reconstructions])
latent_loss = -0.5 * K.sum(
1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss="binary_crossentropy", optimizer="rmsprop", metrics=[rounded_accuracy])
history = variational_ae.fit(X_train, X_train, epochs=25, batch_size=128,
validation_data=(X_valid, X_valid))
# Epoch 1/25
# 430/430 [==============================] - 5s 7ms/step - loss: 0.3895 - rounded_accuracy: 0.8608 - val_loss: 0.3493 - val_rounded_accuracy: 0.8964
# Epoch 2/25
# 430/430 [==============================] - 3s 6ms/step - loss: 0.3426 - rounded_accuracy: 0.8979 - val_loss: 0.3416 - val_rounded_accuracy: 0.9021
# Epoch 3/25
# 430/430 [==============================] - 3s 6ms/step - loss: 0.3326 - rounded_accuracy: 0.9054 - val_loss: 0.3354 - val_rounded_accuracy: 0.9025
# 중략...
# Epoch 23/25
# 430/430 [==============================] - 2s 5ms/step - loss: 0.3125 - rounded_accuracy: 0.9216 - val_loss: 0.3177 - val_rounded_accuracy: 0.9213
# Epoch 24/25
# 430/430 [==============================] - 2s 5ms/step - loss: 0.3123 - rounded_accuracy: 0.9219 - val_loss: 0.3136 - val_rounded_accuracy: 0.9213
# Epoch 25/25
# 430/430 [==============================] - 2s 5ms/step - loss: 0.3121 - rounded_accuracy: 0.9221 - val_loss: 0.3156 - val_rounded_accuracy: 0.9218* encoder, decoder 구성과 최종 autoencoder구성까지의 코드는 이해하기 어렵지 않을 것이다.
* latent loss는 우리가 앞서 살펴봤던 식을 그대로 구현한 것이다. 이 latent loss가 너무 커지지 않도록 조정을 해줘야 할 것이다(조정의 이유는 위에서 언급한 바 있다). latent loss를 reconstruction loss와 비슷하게 scaling해줘야 하는데, autoencoder의 reconstruction loss는 원래 각 픽셀의 reconstruction error의 합을 사용하는데, binary crossentropy를 cost function으로 사용할 때는 단순 합이 아니라 모든 픽셀의 평균을 계산한다. 때문에 모든 픽셀 784(28*28)개의 평균을 reconstruction loss가 사용하므로 latent loss도 이와 비슷하게 784로 나눠줘야 한다. 이 때 배치에 있는 latent loss의 평균을 나눠주는 것이 중요하다.
* latent loss, reconstruction loss 모두 784로 나누기 때문에 최종 손실이 784배 작아지게 된다. 이렇게 손실의 절댓값이 작아질 때는learning rate를 크게 잡는 것이 좋다.
show_reconstructions(variational_ae)
plt.show()
패션 MNIST 이미지 생성하기
def plot_multiple_images(images, n_cols=None):
n_cols = n_cols or len(images)
n_rows = (len(images) - 1) // n_cols + 1
if images.shape[-1] == 1:
images = np.squeeze(images, axis=-1)
plt.figure(figsize=(n_cols, n_rows))
for index, image in enumerate(images):
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(image, cmap="binary")
plt.axis("off")
tf.random.set_seed(42)
codings = tf.random.normal(shape=[12, codings_size]) #noraml distribution에서 coding 생성
images = variational_decoder(codings).numpy()
plot_multiple_images(images, 4)
save_fig("vae_generated_images_plot", tight_layout=False)
* decoder가 normal distribution에서 생성된 coding을 decode하는 것을 학습하였기 때문에 encoder 없이 normal distribution에서 vector를 추출해 decoder에 집어넣으면 위와 같이 이미지를 얻을 수 있다.
* 생각보다 이미지의 퀄리티가 떨어진다고 생각할 수 있지만, 아주 짧은 시간 훈련을 통해 생성된 모델이라는 것을 감안하면 나쁘지는 않다.
Semantic Interpolation(시멘틱 보간)
tf.random.set_seed(42)
np.random.seed(42)
codings_grid = tf.reshape(codings, [1, 3, 4, codings_size])
larger_grid = tf.image.resize(codings_grid, size=[5, 7])
interpolated_codings = tf.reshape(larger_grid, [-1, codings_size])
images = variational_decoder(interpolated_codings).numpy()
plt.figure(figsize=(7, 5))
for index, image in enumerate(images):
plt.subplot(5, 7, index + 1)
if index%7%2==0 and index//7%2==0:
plt.gca().get_xaxis().set_visible(False)
plt.gca().get_yaxis().set_visible(False)
else:
plt.axis("off")
plt.imshow(image, cmap="binary")
save_fig("semantic_interpolation_plot", tight_layout=False)
* 코딩 수준에서의 시멘틱 보간을 하기 위해서는 resize()함수를 사용하면 된다. resize함수는 기본적으로 bilinear interpolation(이중 선형 보간)을 시행한다.
* 박스친 이미지는 원본 이미지이다. 원본 아래 이미지가 나머지 두 이미지를 보간한 이미지이다.
'Deep Learning > Hands On Machine Learning' 카테고리의 다른 글
| 강화학습 기본 (0) | 2022.01.08 |
|---|---|
| GAN(Generative Adversarial Network) (0) | 2022.01.01 |
| 17.7 Sparse AutoEncoder (0) | 2021.12.28 |
| 17.6 Denoising AutoEncoder (0) | 2021.12.26 |
| 17.5 Recurrent AutoEncoder (0) | 2021.12.26 |



