이전에 trasnformer를 정리해 놓은 글이 있으니, 읽기 전에 참고 바랍니다.
https://soki.tistory.com/108?category=1077319
Attention Is All You Need, NIPS 2017 - Transformer 논문 리뷰
* Attention is all you need 논문을 개인적으로 정리해봤습니다. * 중요 내용만을 뽑아 기술했으므로 원문의 의도가 본의아니게 왜곡됐을 수도 있습니다. 만약 틀린 부분이 있다면 댓글로 알려주세요.
soki.tistory.com
https://soki.tistory.com/97?category=1065364
Transformer
Intro * Transformer는 seq2seq의 encoder, decoder를 차용하되, RNN을 제거하고 attention을 사용한 모델이다. * 처음에 transformer에 대한 개괄적인 설명을 보고 여기서 RNN을 제거하고 attention을 사용한 이..
soki.tistory.com
Transformer-XL paper link : https://arxiv.org/abs/1901.02860
1. Introduction
Long-term dependency modeling 변천사
* language model에서 sequential data가 주어졌을 때 long-term dependency를 modeling하는 것은 challenge이다.
* 이를 해결하기 위해 RNN이 개발되었지만, gradient vanishing, explosion 문제가 있었고, LSTM과 gradient clipping 기법이 개발되었다.
* 하지만, LSTM도 실증적으로 최대 200개 정도의 sequence만 다룰 수 있다고 알려져 있기 때문에 long-term dependency 문제를 완전히 해결하지는 못했다.
* 최근 개발된 attention에서는 거리가 먼 단어들간의 관계를 직접적으로 계산할 수 있기 때문에 이러한 long-term dependency를 모델링 하는 것이 가능해졌다.
Fixed length contexts의 문제점
* 또한 최근 보조 손실(auxiliary losses)과deep transformer network를 통해 LSTM 성능을 크게 능가하는 character-level LM이 개발된 바 있다(관련 논문 : https://arxiv.org/abs/1808.04444). 하지만, 이 논문에서는 fixed context length의 segment를 사용했기 때문에 fixed length(사전에 정해놓은 고정길이)를 넘어서는 context의 long-term dependency를 modeling하지 못했다.
* 또한 훈련 데이터셋의 각 segment들이 sentence나 semantic boundary를 고려해 나눠진 것이 아니기 때문에 초반의 몇 개의 단어를 예측하는데 필요한 정보가 부족했다. 이를 본 논문에서는 context fragmentation 문제라고 명명하기로 했다.
Fixed length contexts 문제의 해결 - Transformer XL
1) Introducing notion of recurrence to self-attention
* Deep self-attention network에 recurrence라는 개념을 도입한다. segment 시작할 때 hidden state를 처음부터 다시 계산하는게 아니라, 이전 segment의 hidden state를 다시 사용하는 방법을 사용하는 것이다.
* reused hidden states는 current segment 입장에서 메모리이며, previous segment와 current segment를 연결하는 역할을 한다.
* 결과적으로 information이 segment 단위로 전파되기 때문에 very long-term dependency 또한 modeling하는 것이 가능해지는 것이다. 그리고 이 과정을 통해 context fragmentation 문제도 해결 가능하다.
2) relative positional encoding
* 추가적으로 attention에서 기존의 positional encoding 방식이 absolute positional encoding이었다면, 본 논문에서는 relative positional encoding 방법을 사용한다. relative positional encoding 방식은 training과정에서 사용되었던 길이보다 긴 attention length도 처리 가능하도록 generalize해주는 역할을 한다.
* transformer XL은 RNN보다 character-level, word-level language modeling에서 더 뛰어난 성능을 보이는 첫 번째 self-attention 모델이다.
3. Model
3.1 Vanilla Transformer Language Models
* transformer나 self-attention은 arbitarily long context를 고정 길이의 representation으로 encode한다.
* 메모리와 컴퓨팅 파워의 제약이 없다면 FFNN과 같이 전체 context를 입력으로 사용해 unconditional transformer decoder를 통해 처리할 수 있겠지만, 현실적으로는 불가능하다. 그렇다면 현실적인 방법으로는 어떤게 있을까?

Vanilla Model
* corpus를 다룰 수 있는 크기의 segment들로 분할하는 방법이다.
* segment간의 dependency는 학습 불가능하다.
* vanilla model의 training시의 단점은 아래와 같다.
1) 학습 가능한 가장 긴 dependency는 segment의 길이로 제한된다(segment 길이 이상의 dependency에 대해 학습 불가능하다).
2) 고정 길이의 segment에 sequence를 잘라서 넣으면, 앞서 언급한 context fragmentation problem이 발생한다.
* vanilla model의 evalutation시에는 training시에 문제가 됐었던 context fragmentation문제는 해결된다. 주어진 sequence를 segment단위로 잘라 입력에 사용하는 것이 아니라, window를 하나씩 옮겨가듯 오른쪽으로 1 position씩 옮겨가며 다음 prediction을 시행하기 때문이다.
* 하지만, evalutation의 이 과정은 매우 비용이 많이 든다. 한 position씩 옮겨갈 때마다 이전 입력을 통해 계산했던 hidden state valuee들을 재계산해야되기 때문이다.
3.2 Segment-Level Recurrence with State Reuse

Recurrence scheme to the Transformer
* 앞서 언급했던 vanilla model의 한계점을 해결하기 위해 Transformer에 recurrence 개념을 도입하기로 한다.
* 이전 segment를 통해 계산된 hidden state value들은 저장되고, 다음 segment의 초기 값들을 계산하기 위해 재사용된다. 이를 통해 segment fragementation problem을 해결하고 segment간에도 정보가 흐를 수 있도록 한다.
* 두 연속된 길이가 $L$인 segment들이 아래와 같다고 해보자.
$s_\tau = [x_{\tau, 1}, ... , x_{\tau, L}]$, $s_{\tau+1} = [x_{\tau+1, 1}, ... , x_{\tau+1, L}]$
* $s_\tau$ segment의 n번째 layer의 hidden state sequence가 아래와 같다고 해보자.
$h_\tau^n \in R^{L \times d}$, where d is the hidden dimension
* 이 때 segment $s_{\tau + 1}$의 n번째 layer의 hidden state는 아래와 같이 생성된다.
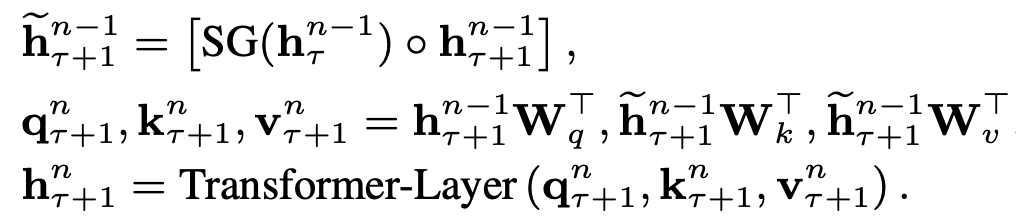
* $SG(\bullet)$ 는 stop gradient를 뜻한다.
* $[h_u \circ h_v]$는 두 hidden sequence를 길이 방향으로(행 방향) concatenate한다는 의미이다.
* $W$는 model parameters이다.
* n번째 key, value matrix들은 $\tilde h_{\tau + 1}^{n-1}$을 통해 생성된다.
* n번째 hidden seuqence는 이렇게 생성된 n번째 key, value와 query를 통해 생성된다.
* 이러한 연속된 두 segment간의 recurrence mechanism을 통해 전체 segment들간의 dependency를 모델링할 수 있다.
* 주의할 점으로는 이러한 recurrence dependency는 conventional RNN-LM과 같이 같은 layer들 간의 dependency가 아닌 n번째 layer와 n-1번째 layer간의 dependency라는 점이다.
* 동일 layer가 아닌 n번째와 n-1번째 layer의 dependency가 전파되기 때문에 최대로 모델링 가능한 dependency는 $length * layer$로 제한된다. 위 그림 자료에서는 segment의 길이가 4이고, layer가 3개이기 때문에 12길이의 dependency가 모델링 가능하다.
* 지금까지 설명한 과정은 truncated BPTT와 비슷하지만, 다른 점은 마지막 hidden state대신 hidden state의 sequence를 캐싱한다는 것과, relative positional encoding을 사용한다는 점이다.
* transformer에 recurrence 개념을 도입함으로서 앞서 언급한 장점들을 달성할 수 있지만, 한 편으로는 이전 segment에서 사용되었던 hidden state들을 캐싱해놓았다가 다음 segment에서도 사용하기 때문에 추론 속도 또한 vanilla model보다 1800배 정도 빠르다.
Predefined length
* 이를 $m_\tau^n \in \mathbb R^{M \times d}$ 라고 정의한다.
* 실제 실험에서는 이 M의 크기를 초기에 segment와 동일하게 설정하고(바로 이전 segment만 extra context로서 사용함) M의 크기를 점점 늘리면서 evaluation을 시행하였다.
3.3 Relative Positional Encoding
Transformer-XL에 Absolute Positional Encoding을 적용할 때의 문제점
* 이렇게 이전 segment의 정보를 이용하여 long-term dependency를 모델링할 방법을 찾아냈지만, 한 가지 문제가 있다.
* transformer 구조에서 각 input들의 위치 정보는 absolute positional encoding을 통해 계산된다.
* 만약 이 absolute positional encoding을 본 논문에서 고안한 방법에 적용하면 어떻게 될까?
* 먼저 positional encoding을 아래와 같이 정의해보자.
$U \in \mathbb R^{L_{max} \times d}$
* i번째 row $U_i$는 i번째 abosolute position에 해당한다.
* $L_{max}$는 모델 가능한 최대 sequence길이를 의미한다.
* 이 positional encoding과 input sequence가 더해진 형태의 matrix가 transformer의 input으로 입력된다. absolute positional encoding을 recurrence mechanism에 적용해보자.
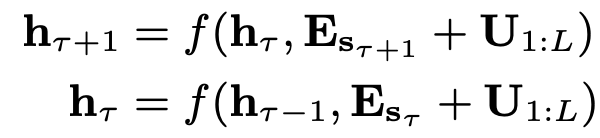
* $E_{s_\tau} \in \mathbb^{L \times d}$ 는 sequence $s_\tau$의 word embedding이다.
* function $f$는 transformation function을 뜻한다.
* 위 식에서 더해지는 positional encoding을 살펴보자. $E_{s_\tau}$와 $E_{s_{\tau+1}}$에 모두 동일한 positional encoding $U_{1:L}$이 더해지는 것을 볼 수 있다.
* 동일한 위치정보가 sequence에 더해지므로 모델은 $x_{\tau, j}$($\tau 번째 sequence의 j번째 token$)와 $x_{\tau+1, j}$의 위치정보의 차이를 확인하지 못하게 된다.
문제 해결을 위한 방법 - relative positional encoding
* positional encoding의 컨셉은 모델에게 temporal clue 혹은 bias(어디에 집중할지)를 제공하는 것이다.
* 방금 언급한 목적을 달성하기 위하여 bias를 initial embedding에 포함시키는 것(absolute positional encoding의 방법) 대신에 각 layer의 attention score에 정보를 주입하는 방법을 사용할 수 있다.
* 예를 들어 query vector $q_{\tau, i}$는 key vector $k_{\tau \leq i}$에 집중할 때를 보면, key vector의 절대적인 위치를 알 필요가 없다. 대신 각 key vector $k_{\tau, j}$와 query vector $q_{\tau, i}$의 상대적인 거리만 알면된다(i.e $i-j$).
* 이 방법을 통해 relative positional encoding을 생성해보자.
* $R \in \mathbb R^{L_max \times d}$의 i번째 row인 $R_i$는 두 position 간의 i 거리를 나타낸다.
* Standard Trasnformer의 attention score는 아래와 같이 계산된다.
$A_{i,j}^{abs} = (E_{xi}^T + U_i^T) W_q^T ((E_{xj}^T + U_j^T)W_k^T)^T$
* 논문에서는 위 식을 생략하고 위 식을 전개한 식인 아래 식부터 소개한다.

* relative positional encoding을 적용하면 기존의 식을 아래와 같이 바꿀 수 있다.
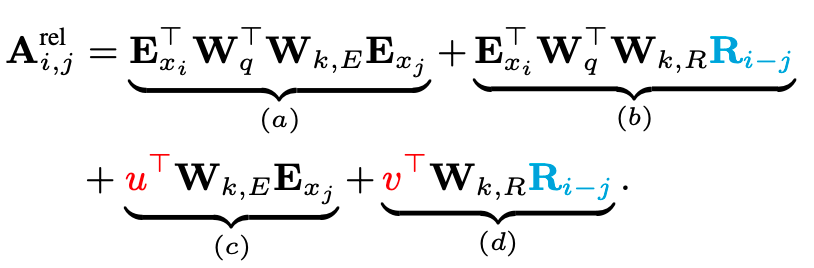
* 위 변경된 식의 내용은 아래와 같다.
1) replace all $U_j$ to $R_{i-j}$
* 모든 j에(key에) 대한 absolute positional encoding을 i와 j간의(query와 key간의) relative positional encoding으로 변경한다.
* 여기서 relative positional encoding R은 sinusoid encoding matrix이다.
2) replace $U_i^T W_q^T$ to $u \in R^d$
* 두 번째로 $U_i^T W_q^T$를 모두 동일하게 $u \in \mathbb R^d$로 변경해주었다.
* 즉 모든 query들의 position $i=0~L_max$ 에서 동일한 positional encoding을 사용하겠다는 뜻이다. 더 자세히 설명하자면, 이는 relative positional encoding이 query vector와 key vector 사이의 상대적 거리만을 측정하기 때문에 각 query vector의 position은 고정값을 사용하게 된다.
3) Seperate weight matrix
* weight matrix $W_k$를 그대로 적용하지 않고, $W_{k, E}$, $W_{k, R}$로 분리해 각자 다른 weight matrix를 훈련시켜 다른 값의 content-based key vector와 location-based key vector를 도출해낸다.
* 이렇게 파라미터를 변경함으로서 각 term들(a, b, c, d)은 다음과 같은 직관적 의미를 가지게 된다.
a) content-based addressing
b) content-dependent positional bias
c) governs a global content bias
d) global positional bias
* 이렇게 새롭게 바뀐 fomula에서 유도된 bias들 덕분에 훈련시 모델의 메모리에 더 길게 남아있을 수 있게 된다.
Transformer-XL architecture의 완성

* N 개의 layer와 single attention head를 가진 trasnformer-xl 모델을 요약하면 위와 같다.
* $n = 1, ..., N$이다.
*
$h_\tau^0 := E_{s_\tau}$는 초기 word embedding으로서 사용된다.
* Attention score 전체를 구하는데는 모든 (i, j)쌍에 대하여 $W^n_{k, R} R_{i-j}$를 구해야 한다.
* 이 때 cost는 sequence length에 대해 quadratic 이다. 하지만, $i-j$의 값이 0부터 sequence length로 제한되기 때문에 아래와 같은 계산을 통해 cost를 quadratic에서 linear로 줄일 수 있다.
Appendix-B : Efficient Computation of the Attention with Relative Positional Embedding
4. Experiemnts
4.1 Main Results
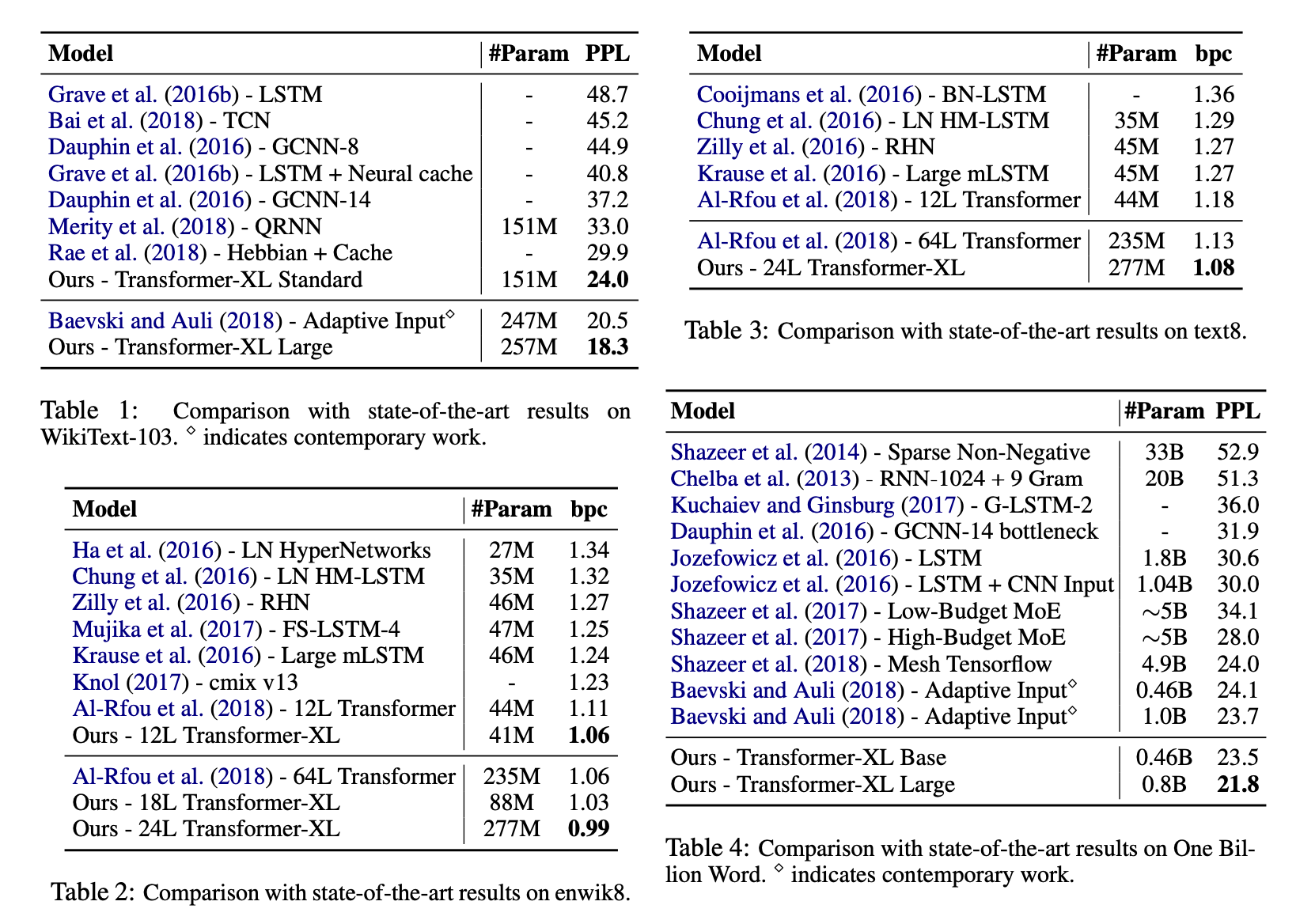
* Transformer-XL을 다양한 데이터셋에서 word-level, character-level 로 비교하였다.
'Deep Learning > 논문정리' 카테고리의 다른 글
| XLNet : Generalized Autogregressive Pretraining for Lanuguage Understanding(NIPS 2019) (0) | 2022.05.09 |
|---|---|
| Deep Contextualized Word Representation, NAACL 2018 (ELMO 논문 리뷰) (0) | 2022.04.29 |
| Attention Is All You Need, NIPS 2017 - Transformer 논문 리뷰 (0) | 2022.04.03 |
| GloVe : Global Vectors for Word Representation (0) | 2022.02.12 |
| Indexing by Latent Semantic Analysis(LSA) (0) | 2022.02.11 |



