* 행렬은 여러 개의 숫자로 이뤄져있기 때문에 부호나 크기를 정의하기는 어렵지만 유사한 개념은 정의할 수 있다.
정부호와 준정부호
양의 정부호(positive definite)
* 영 벡터가 아닌 모든 벡터 x에 대해 다음 부등식이 성립하면 행렬 A가 양의 정부호라고 한다.
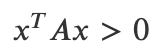
* 만약 비교 연산자에 등호가 포함되어 있으면 양의 준정부호라고 한다.
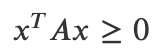
* 이 방법으로 모든 행렬에 대해 양의 정부호, 준정부호를 정의할 수 있지만, 보통 대칭행렬(대각선 기준 대칭인 행렬)에 대해서만 정의한다.
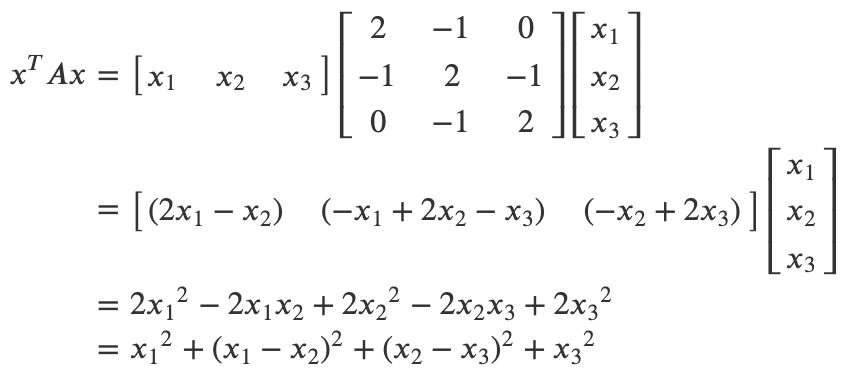
* 이 값은 x가 영벡터인 경우를 제외하고는 항상 0보다 크다. 이 경우 행렬 A는 양의 정부호에 해당한다.
행렬 Norm
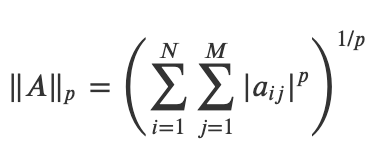
* 행렬의 norm에는 여러 정의가 있는데 여기에서는 entrywise matrix norm의 정의를 따른다.
* 위 식은 행렬의 norm에 대하여 정의한 식이다.
* p값은 보통 1,2, 혹은 $ \infty $ 가 사용된다. p가 2일 경우가 가장 많으며 이 경우 Frobenius norm이라고도 부르며 p에 2 대신 F를 표기한다. 놈의 p값에 대한 언급이 없는 경우 2라고 생각하면 된다.
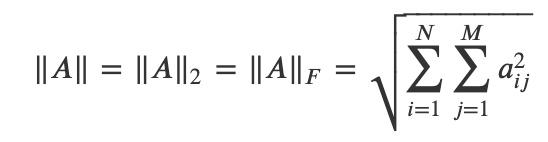
* norm은 항상 0보다 크거나 같다.
* norm은 벡터에 대해서도 정의 가능하다. 벡터의 norm에서 중요한 성질은 벡터의 norm의 제곱이 벡터의 제곱합과 동일하다는 것이다.

* norm의 제곱은 행 벡터 norm의 제곱의 합 또는 열 벡터 norm의 제곱의 합과 같다.
norm의 정의
1) norm의 값은 0 이상이다. 영행렬일 때만 norm의 값이 0이 된다.
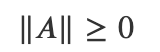
2) 행렬에 scalar를 곱하면 norm의 값도 그 scalar의 절대값을 곱한 것과 같다.
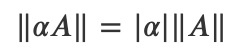
3) 행렬의 합은 norm은 각 행렬의 norm의 합보다 작거나 같다.

4) 정방행렬의 곱의 norm은 각 정방행렬의 norm의 곱보다 작거나 같다.

대각합(Trace)

* 대각 원소들의 합을 뜻하며, 정방행렬에 대해서만 정의된다.
* 만약 행렬이 NxN 항등행렬일 경우 대각합은 N이 된다.
* 대각합은 norm과 달리 단순 덧셈이므로 음수가 될 수 있다.
대각합 성질
1) scalar를 곱하면 대각합은 scalar와 원래 대각합의 곱이다.
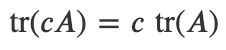
2) 전치연산을 해도 대각합이 달라지지 않는다.

3) 두 행렬의 합의 대각합은 두 행렬의 대각합의 합이다.
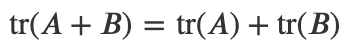
4) 두 행렬의 곱의 대각합은 행렬의 순서를 바꾸어도 달라지지 않는다.
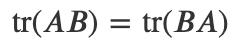
5) 세 행렬의 곱의 대각합은 다음과 같이 순서를 순환시켜도 달라지지 않는다.

* 5번 성질은 trace trick이라고 부르며 이차 형식의 미분을 구하는데 유용하게 사용된다. A,B,C 행렬이 각각 정방행렬일 필요는 없고, 최종적으로 대각합을 구하게 되는 행렬만 정방행렬이면 된다.
* 이차형식의 trace trick 공식은 다음과 같다.

norm과 trace의 관계
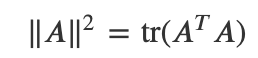
A=np.array([[1,2],
[3,4]])
print(np.linalg.norm(A.T@A)) # 29.866369046136157
print(np.trace(A.T@A) # 30행렬식(determinant)
* 정방행렬 A의 행렬식은 $det(A), detA, |A|$로 표시한다.
1) 행렬 A가 1 x 1 즉 scalar인 경우 행렬식은 자기 자신이 된다.
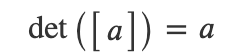
2) 행렬 A가 scalar가 아니라면 여인수 전개(confactor expansion) or 라플라스 전개(Laplace expansion)라고 불리는 다음 식을 이용해 계산한다.
* 여인수 전개 식은 아래와 같다. 두 식 모두 결과는 같기 때문에 어떤 식을 사용하여도 상관 없다.
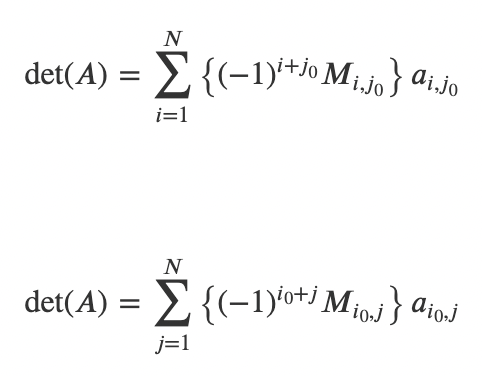
* $i_0 or j_0$는 임의로 선택한 행 or 열을 뜻한다.
* 원소 앞에 있는 수식은 가중치로 $M_i,j$는 minor(소행렬식)이라고 부르는 i행과 j열을 지워서 얻어진 행렬의 행렬식이다. 이 행렬의 경우 원래의 행렬보다 크기가 1이 작게 된다.
* 이 minor 또한 위의 정의를 통해 행렬식을 전개하게 된다. 이를 반복하면 scalar값인 행렬이 나오는데 이 행렬식의 값은 자기 자신이 된다. 때문에 행렬식을 구하는 방법은 recursive하다.
* 식의 이해를 돕기 위해 아래 행렬을 통해 계산해본다.
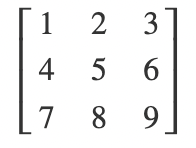
* 만약 첫 번째 열을 선택해 $j_0 = 1$ 이라고 하면, 이 행렬의 행렬식은 아래와 같이 계산된다.

* 여기서 $M_{1,1}$은 아래와 같이 계산된다.

* $M_{1,1}$ 이 scalar값이 아니므로 다시 여인수 전개를 실시한다.
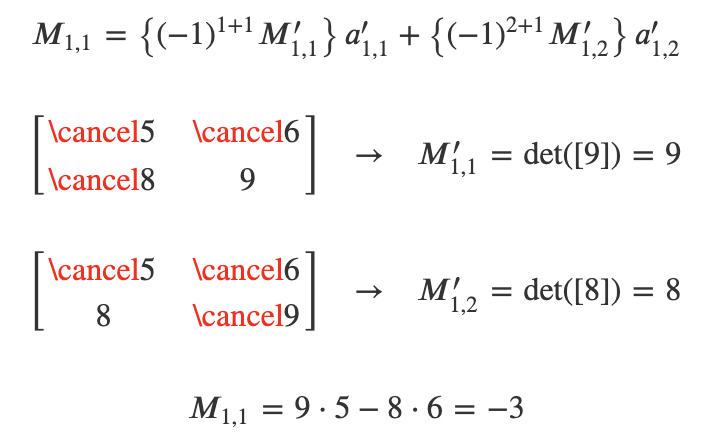
* 이와 같은 방법으로 나머지 minor들도 계산하고 나면 다음과 같이 행렬식의 값을 구하게 될 수 있다.
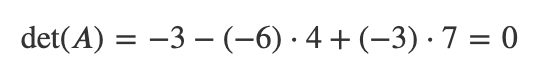
A=np.array([[1,2,3],
[4,5,6],
[7,8,9]])
np.linalg.det(A) #0.0* python에서는 det() 메소드를 통해 쉽게 구현할 수 있다.
행렬식의 성질
1) 전치 행렬의 행렬식은 원래의 행렬의 행렬식과 같다.
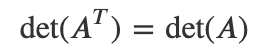
2) 항등 행렬의 행렬식은 1이다.

3) 두 행렬의 곱의 행렬식은 각 행렬의 행렬식의 곱과 같다.
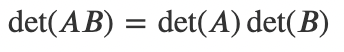
4) 역행렬 $A^-1$은 원래의 행렬 A와 다음 관계를 만족하는 정방행렬을 말한다. I는 항등행렬이다.
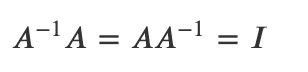
5) 역행렬의 행렬식은 원래의 행렬의 행렬식의 역수와 같다.
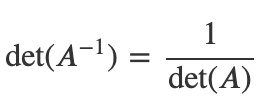
6) 역행렬의 행렬식은 원래의 행렬의 행렬식의 역수와 같다.
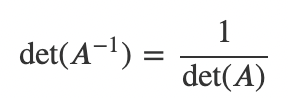
'수학 > Numpy로 공부하는 선형대수' 카테고리의 다른 글
| 선형대수와 해석기하의 기초 (0) | 2021.11.22 |
|---|---|
| 선형 연립방정식과 역행렬 (0) | 2021.11.18 |
| 벡터와 행렬의 연산 (0) | 2021.11.12 |
| 데이터와 행렬 (0) | 2021.11.12 |



