Entropy, KL Divergence, Cross Entropy 한방정리
https://www.youtube.com/watch?v=Dc0PQlNQhGY
너무 훌륭한 정리 영상을 유튜브에서 보고 참고해서 작성합니다. 더 자세한 강의는 해당 유튜브 링크를 참조해주세요!
Entropy의 정의
* Entropy는 정보이론에서 사용되는 용어로 '놀라움의 정도'로 표현 가능하다.
* 해가 뜨는 경우를 생각해보자.
* 해가 뜨는 경우 = {'동쪽에서 뜬다', '서쪽에서 뜬다'}
* 당연히 서쪽에서 뜰 확률은 매우매우매우매우 적을 것이다.
* 만약 해가 서쪽에서 떴다는 관측이 주어진다면 이는 '놀라움의 정도'가 매우 크기 때문에 정보량이 높다고 볼 수 있다.
* 예시에서 살펴볼 수 있듯이 '놀라움의 정도'는 발생확률의 크기와 반비례한다.
* ' 발생확률이 적다 = 놀라움의 정도가 크다 = 정보량이 많다 ' 로 정리할 수 있겠다.
* 아래와 같은 일반화된 정리도 도출 가능하다.
확률변수 $X$가 주어졌고, 발생확률이 $P(x)$ 가 주어졌을 때, 정보량에 대한 함수를 $h(x)$ 라고 가정한다면,
h(x) = f(p(x)) 의 관계가 성립한다.
이 때, 함수 f(x)는 monotonic decrease function이다.
정보량 함수 정의
* 자, 그러면 여기서 주어진 확률을 통해 정보량을 계산하는 함수 $f(x)$는 어떻게 정의해야 할까?
* 아래와 같은 과정을 통해 적절한 함수 $f(x)$를 도출해낼 수 있다.
1) 가정 : 두가지 경우의 수를 갖는 확률변수 X, Y가 주어졌다고 해보자. 두 확률변수는 독립이다.
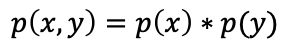
2) 두 확률변수가 독립이기 때문에 위와 같은 관계가 성립한다.
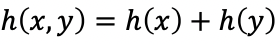
3) 독립인 사건의 정보량은 두 사건이 동시에 발생했다고 측정하던, 따로 발생했다고 측정하고 더하던 같기 때문에 위와 같은 관계가 성립한다.
3-1) 예를 들어 h(해가 동쪽에서 떴다, 내가 오늘 치킨을 먹었다) = h(해가 동쪽에서 떴다) + h(내가 오늘 치킨을 먹었다) 의 관계는 성립한다.
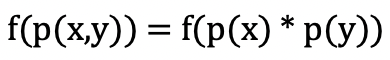
4) 3)에서 살펴본 바에 의하면 위와 같은 관계가 성립한다.
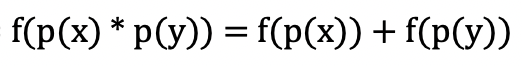
5) 그런데, $f(p(x, y)) = h(x)$이다. 때문에 위와 같은 관계가 성립한다.
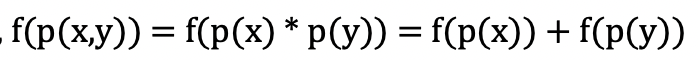
6) '4)'와 '3)'을 정리해보면 위와 같은 관계가 성립한다.
7) 자 이제 그러면 $f(x)$로 적절한 함수에 대해 생각해보자. '6)'을 만족하기 위해서는 log함수가 사용되어야 할 것이다. log(a*b) = log(a) + log(b) 이기 때문이다.
8) 또한 $f(x)$는 앞에서 말했듯이 monotone decreasing이기 때문에 $x$ 값이 증가할수록 $f(x)$ 값이 작아져야 한다. 이를 위해 log 함수 앞에 마이너스를 붙여야 할 것이다.
9) 결론적으로 이를 만족하는 $f(x)$는 $-log_2 x$ 가 된다.
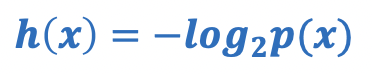
10) 이에 따라 위 식이 정의 가능하다.
Entropy 함수 정의
* 정보량에 대한 함수를 정의했다.
* Entropy는 '평균적인 정보량'에 관심을 가진다.
* 따라서 '정보의 발생확률 X 정보량'을 모두 합해 평균 정보량인 Entropy를 구할 수 있다.
1) 확률변수가 이산형일 경우
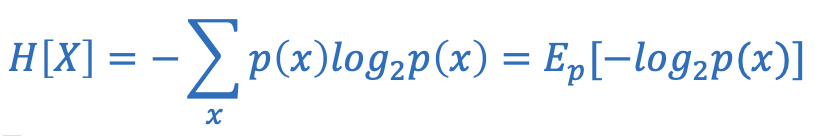
2) 확률변수가 연속형일 경우
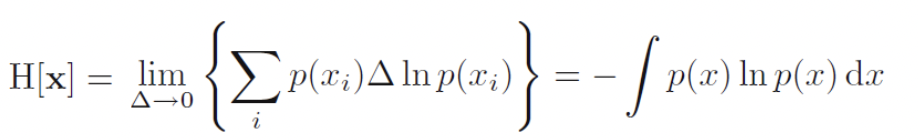
Entropy 예시
* 정팔면체 주사위가 존재한다고 해보자.
* 각 면이 위로 올 확률이 동일할 경우와 각 면이 위로 올 확률이 모두 동일하지 않을 경우의 Entropy를 계산해보자.
1) 각 면이 위로 올 확률이 동일
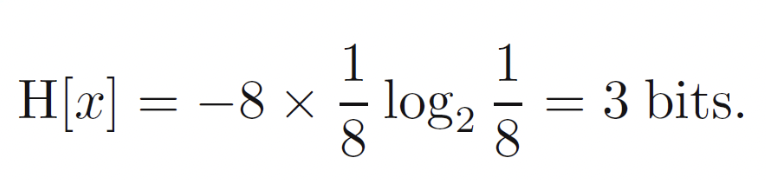
* 각 면이 위로 올 확률이 1/8로 동일하다고 했을 때 Entropy는 위와 같이 계산 가능하다.
2) 각 면이 위로 올 확률이 동일하지 않을 경우
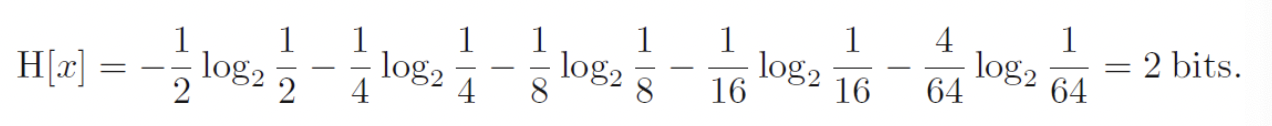
* 예를 들어 (1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64) 의 확률분포를 가질 때 위와 같이 계산 가능하다.
결론)
* 이산형 확률변수일 경우 가장 Entropy가 높아지는 경우는 각 사건의 발생 확률이 모두 동일할 경우이다.
* 직관적으로 생각해봐도, 모든 사건의 발생확률이 동일해 어떤 사건이 발생할지 예측하기 쉽지 않을 경우 '놀라움의 정도'인 Entropy가 커지는게 맞을 것이다. 던질 때 마다 1이 나오는 주사위를 굴렸을 때 어짜피 1이 나올것으로 예상되기 때문에 '놀라움의 정도'는 매우 작을 것이다.
* 만약 확률변수가 연속형일 경우엔 확률분포가 Gaussian Distribution의 형태를 띨 때 가장 Entropy가 높아지게 된다.
KL Divergence
* KL Divergence는 두 확률분포간의 차이를 수치로 나타내는 함수이다.
* 그런데 여기서 두 확률분포는 무엇이고, 무슨 차이를 수치화 한다는 것일까? 지금부터 알아보자.
1) 두 확률분포?
* 여기서 말하는 두 확률분포는 (예측된 확률분포, 실제 확률분포) 를 뜻한다.
* 여기서 예측된 확률분포는 우리가 모델링을 통해 도출한 확률분포가 된다.
2) 무슨 차이를 수치화 하는걸까?
* 결론부터 말하자면, 예측된 확률분포로 인해 발생하는 '잘못계산된 정보량'과 '실제 정보량'의 차이를 수치화 한다.
* 앞서 살펴봤듯이 '확률변수 X의 정보량'은 P(X)를 사용해 도출하게 된다.
* 우리가 P(X) 즉, 확률분포를 잘못 예측하게 되면 결국 확률변수 X의 정보량을 잘못 도출하게 되는 것이다.
* 정보량을 잘못 도출하는 것은 정보를 송수신하는데 드는 비용의 최적화를 방해한다.
3) 왜 두 확률분포간의 차이를 수치화 할까?
* 당연한 얘기지만 두 확률분포 사이의 차이를 최소화 하기 위해서이다.
* 최소화할 대상이 되는 KL Divergence는 때문에 '목적함수'로서 사용될 수 있다.
4) KL Divergence 수식
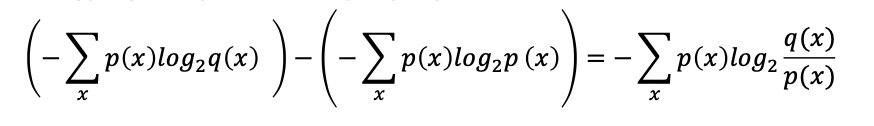
* 여기서 p(x)는 실제 확률분포이고, q(x)는 예측된 확률 분포이다.
Cross-Entropy
* 이제 마지막 단계로 Cross-Entropy에 대해 살펴보자.

* Cross-Entropy의 KL Divergence의 일부 term만을 사용한다.
* KL Divergence를 최소화 하기 위해 q로 미분하면 어짜피 H(p)는 상수취급되어 사라지기 때문이다.
* 결국 H(p, q)을 최소화 하는 것과, KL Divergence 전체를 최소화 하는 것은 동일하게 취급될 수 있다.
* 이러한 이유 때문에 Cross Entropy 식에서는 KL Divergence의 일부 term만을 가져와 사용하는 것이다.
* 참고로 Cross-Entropy는 multi-class classfication에서 loss function으로 사용된다. 그런데 왜 Cross-Entropy를 loss function으로 사용할까?
* multi-class를 수학적으로 표현하기 위해 우리는 One-Hot Encoding을 사용한다.
* One-Hot 벡터는 model을 거쳐 예측되는 확률분포를 출력하게 된다. 예를들면 이렇게 말이다.
[0.1, 0.1, 0.1, 0.1, 0.3, 0.3]
* 우리는 ground truth 인 확률분포와 이 예측된 확률분포의 차이를 계산해서 최소화 하는 방향으로 모델을 update하길 원한다.
* 그래서 loss function으로 Cross-Entropy를 사용하는 것이다.